기상 기후 강의 노트

● 확률변수 X와 Y의 결합분포가 아래와 같을 때, 아래 물음에 답하시오.

(1) X와 Y의 공분산은?

답: 

E(X)=0.5;      E(X^2)=0.5 따라서 V(X)=0.25

E(Y)=1;      E(Y^2)=1 따라서 V(Y)=1

Cov(X, Y) = E(XY) - E(X)E(Y) = 0.6 - 0.5 x 1 = 0.1

(2) X와 Y의 상관계수는? 

답:

Corr = 0.1 / (0.5 x 1) = 0.2

● 하나의 동전을 세번 던졌을 때 나오는 뒷면의 수를 X, 처음  두 번의 시행에서 나오는 앞면의 수를 Y라 하였을 때, 아래 물음에 답하시오.

(1) 두 확률변수 X, Y의 공분산은?

답: 

Cov(X, Y) = E(XY) - μ_x μ_y = 1 x 1/4 + 2 x 1/4 + 2 x 1/8 - 3/2 x 1 = -0.5

(2) 두 확률변수 X, Y의 상관계수는? 

답:

V(X) = npq = 3 x 1/2 x 1/2 = 3/4

V(Y) = npq = 2 x 1/2 x 1/2 = 1/2

따라서, Cov(X,Y)/sqrt(V(X) V(Y)) = -0.5/sqrt(3/4 x 1/2) = -sqrt(2/3)

1. 베르누이 분포

서로 상반되는 두 가지 결과(성공, 실패) 또는 (앞면, 뒷면), (불량품, 양호품) 등으로 이루어진 통계실험에서 성공의 가능성이 p (0 ≤ p ≤ 1)이라 하고, 확률변수 X를 성공이면  X = 1, 실패이면 X = 0이라 할 때, X의 확률분포를 모수 p인 베르누이 분포(Bernoulli distribution)라 하고 X ~ B(1, p)로 나타낸다.

2. 이항분포

매 시행에서 성공률이 p, (0 < p < 1)인 베르누이 시행을  n번 독립적으로 반복시행할 때, 성공한 횟수 X의 확률분포를 모수가 n, p인 이항분포(binomial distribution)라 하고, X ~ B(n, p)로 나타낸다.

베르누이 시행은 2가지 결과로 나타나며, 이항분포는 동일한 베르누이 시행을 독립적으로 n번 행한 것.

● 다음 확률변수 X에 대하여 기대값과 분산을 수식으로 정의하시오.

(1) 이산확률변수 X의 기대값 E(X)

(2) 이산확률변수 X의 분산 Var(X)

(3) 연속확률변수 X의 기대값 E(X)

(4) 연속확률변수 X의 분산 Var(X)

● 결합확률밀도 함수 f(x,y)에 대해 다음을 정의하시오

(1) ∑_y f(x,y)

(2) ∫_-∞^∞ f(x,y) dy

(3) ∑_x f(x,y)

(4) ∫_-∞^∞ f(x,y) dx

(5) X와 Y가 독립이면 f(x,y)

(6) f(x|y)

(7) 이산확률변수 X와 Y에 대해 E(X|y)

(8) 연속확률변수 X와 Y에 대해 E(X|y)

(9) E_Y[E(X|Y)]

(10) E_X[E(Y|X)]

● 다음 표는 2020년도 기상사업 전망으로, 예상되는 성잘률에 대한 확률을 나타내는 것이다. 이 표로 부터 기대괴는 성장률을 구하면? 

답:

성장률(a)가 나타날 확률이 p일때 기대갑은 a x p 이다. 

5% x 0.6 = 3%; 10% x 0.3 = 3%; 15% x 0.1 = 1.5%

따라서, 3개를 합치면 7.5%

●

기대값의 성질

E(X) = μ

E(a X) = a E(X), 단 a는 상수

E(X + b) = E(X) + b, 단 b는 상수

E(X + Y) = E(X) + E(Y)

E[(ab(X) + cd(Y)] = a E[b(X)] + c E[d(Y)], 단 a, c는 상수

E(ab XY) = ab E(XY), 단 a,b는 상수 (만약, 독립이면 E(ab XY)  = ab E(X) E(Y) )

분산의 성질

Var(X) = E[(X-μ)²] = E(X²) - [E(X)]²

Var(a) = 0, 단 a는 상수

Var(aX) = a² Var(X), 단 a는 상수

Var(a + b X) = b² Var(X), 단 a와 b는 상수

Var(aX + bY) = a² Var(X) + b² Var(Y) + 2ab Cov(X,Y), 단 a와 b는 상수

Var(aX - bY) = a² Var(X) + b² Var(Y) - 2ab Cov(X,Y), 단 a와 b는 상수 (만약, 독립이면 Cov(X,Y)=0)

1. 이산형 분포의 기댓값

확률변수 X의 치역이 R이고  이산형 분포를 갖는다고 가정하자.

이때 다음이 성립하면 확률변수 X는 기댓값이 존재한다.

다음 값을 X의 기댓값(expectation)이라 한다.

어느 복권의 상금을 확률변수 X로 하여 다음과같은 확률분포를 생각해 보자.

확률변수의 기대값

X의  분포로부터 직접 기댓값을 구하는 경우

2. 기대값의 성질

3. 분산

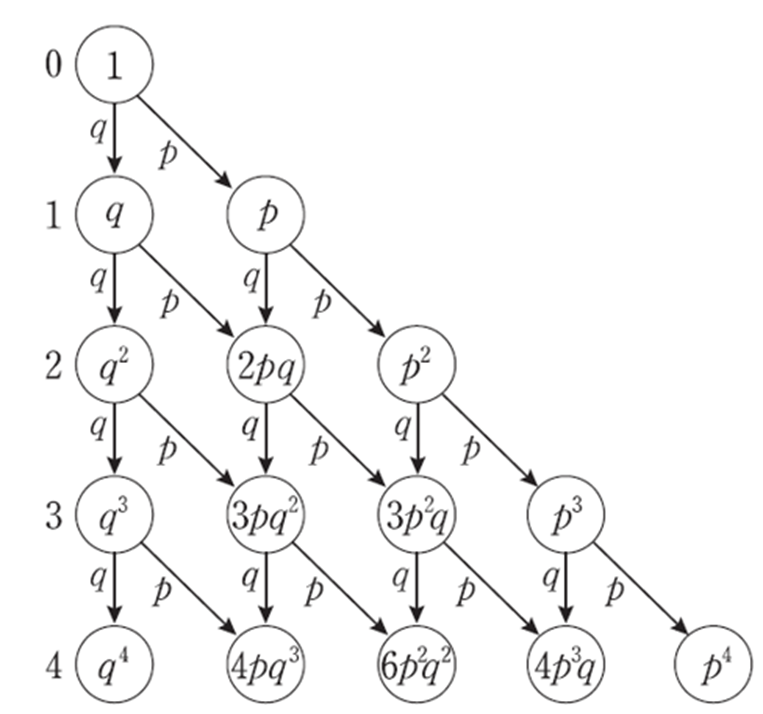
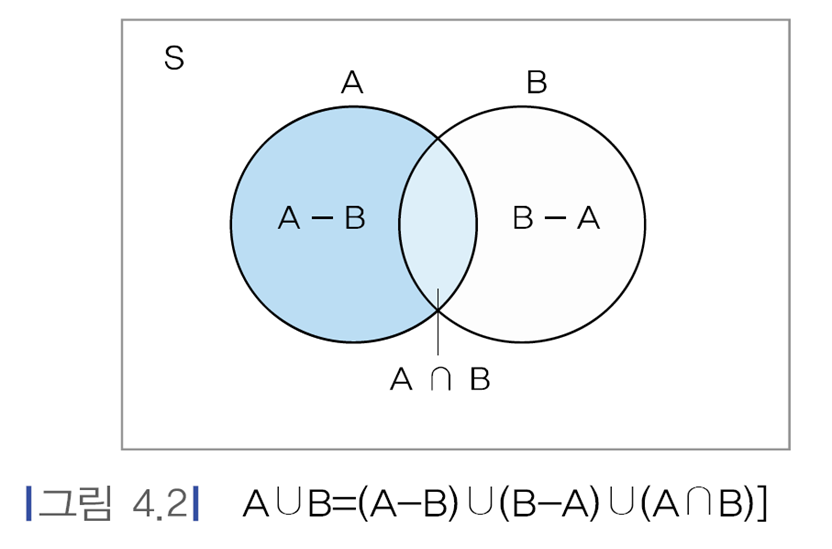
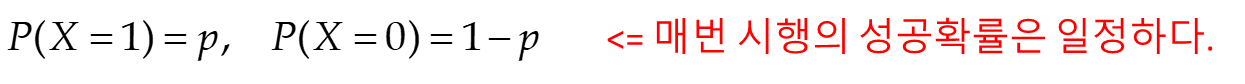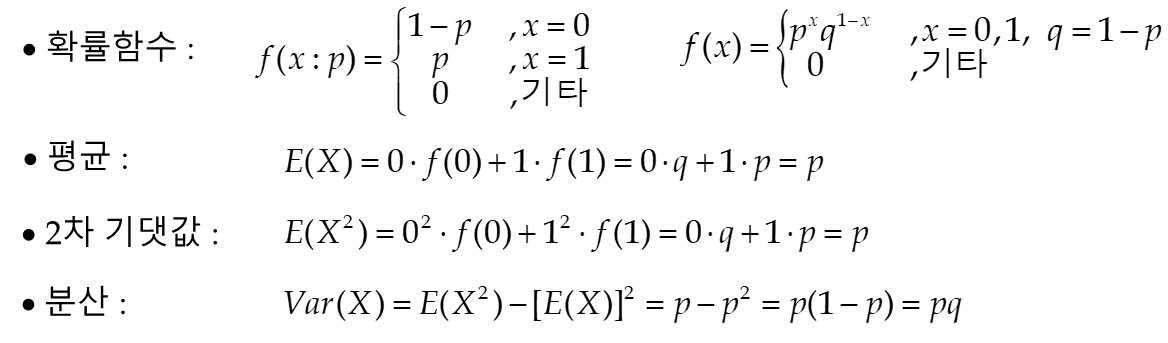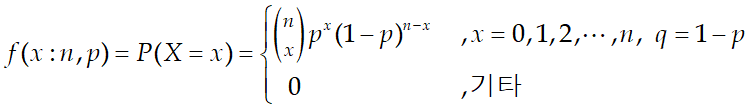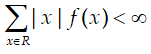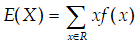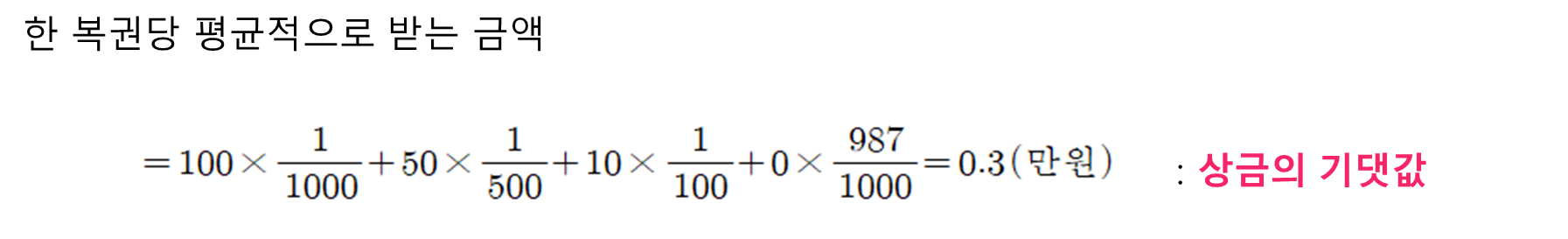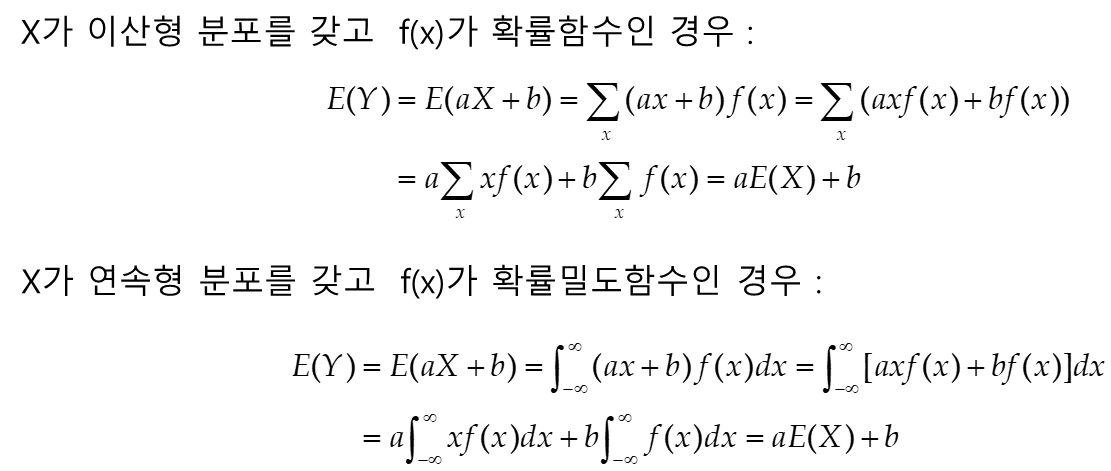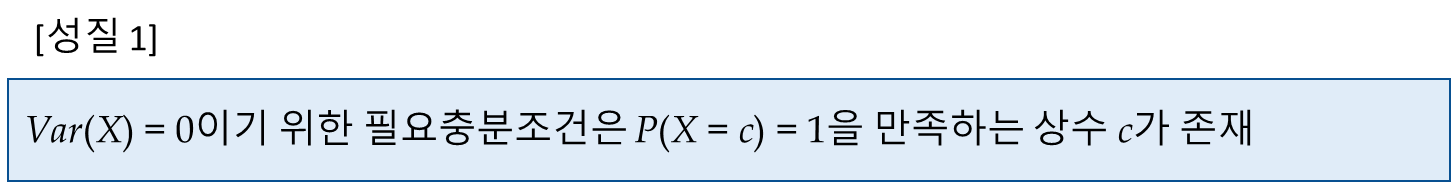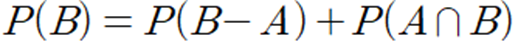● 다음 값을 구하시오. 

0! = 

_nP₀ = 

_nP_n = 

_nC₀ =

_nC_n = 

● x의 확률함수 f(x)가 다음과 같을 때, (x-1)의 기대값은?

답:이산확률변수의 기대값의 성질 E(nX+b) = aE(X)+b

E(X) = ∑ xif(x) = (-1x1/8)+(0x1/8)+(1x2/8)+(2x2/8)+(3x2/8) = 11/8

E(X-1) = E(X)-1 = 3/8

● 주사위를 던져 나온 눈의 수를 X라 하면 X의 기대값은?

답:

E(X) = ∑ xif(x)  = 1x1/6+2x1/6+3x1/6+4x1/6+5x1/6+6x1/6=3.5

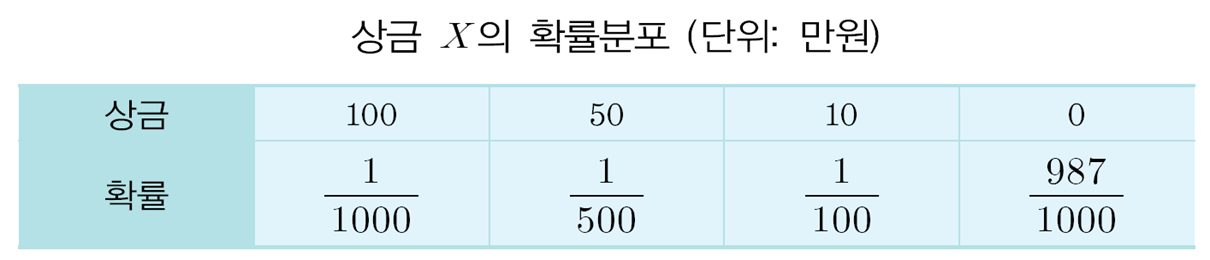
● 아래 표의 확률분포에 대한 기대값은

답: 

E(X) = ∑ xif(x) =1.1

● 구간 [0,1]에서 연속인 확률변수 X의 확률밀도함수가 f(x)=1일때, X의 평균은?

답:

E(X) = ∫ xf(x)dx = ∫10 x dx = [1/2 x2]10 = (1/2 - 0)=1/2

● X,Y의 결합분포함수는 f(x,y) = xy²/13 (x,y)=(1,1)(1,2)(2,2)이고 U,V의 결합분포함수는 g(u,v) = uv²/30 (u=1,2,3; v=1,2)이다. (1) X,Y는 서로 독립인가? (2) U,V는 서로 독립인가?

답:

f(x)f(y)≠f(x,y)이므로 X,Y는 서로 독립이 아니다

g(u)f(v)=g(u,v)이므로 U,V는 서로 독립이다.

● 기대값 E(X) = 3, E(X²) = 30 일때, 분산 var(X)는?

답: var(X)  = E(X²) - [E(X)]² = 30 - 9 = 21

● 우리나라에서 해마다 줄어들고 있는 멸종위기 종 두루미의 개체수를 파악하기 위하여 한 연구소에서 2019년에 200마리의 두루미를 포획하여 다리에 GPS추적기를 붙였다. 2020년에 50마리의 두루미를 잡아 확인해 보니 20마리에서 태그를 발견할 수 있었다. 우리나라의 두루미의 개체 수는 얼마인가?

답: 포획 재포획x : 200 = 50:20 ==> x= 500

● 결합확률밀도함수가 0<y<x<1일때 f(x,y) = 6x이고 나머지 조건인 경우 0으로 주어졌다면 E[E(Y|X)]는?

답: 조건부 기대값의 기대값

fx(x) = ∫x0 6x dy = [6xy]x0 = 6x2       (0<x<1)

fy(y) = ∫1y 6x dx = [3x2]1y = 3 - 3y2  (0<y<1)

E[E(Y|X)] = E(Y)이므로

E(Y) = ∫10 y(3 - 3y2)dy = ∫10 (3y - 3y3)dy = [3/2 y²]10 - [3/4 y⁴]10 = 3/2 - 3/4 = 3/4

● 확률변수 X의 분포가 다음과 같다. 

(1) 기대값을 구하라.

답:

E(X)  = (-2)(0.1) + (-1)(0.2) + 0(0.4) + 1(0.2) + 2(0.1) = 0

(2) Y=X² 라고 할때, E(X)=E(Y)=E(X²) 을 계산하고, E(X²)=[E(X)]² 임을 확인하라

답:

E(X²) = (-2)2(0.1) + (-1)2(0.2) + 02(0.4) + 12(0.2) + 22(0.1) = 1.2 이다. 그러나, (1)에서 기대값의 제곱은 [E(X)]2 = 02 = 0 이므로 제곱의 기대값 1.2와 다르다.

(3) Y의 확률분포를 구하고 이로부터 E(X)=E(Y)=E(X²)을 계산하라. 

답:

이므로, E(Y) = 0(0.4) + 1(0.4) + 2(0.4) = 1.2 로서, (2)에서 구한 결과와 일치한다.

(4) 분산 var(X)를 구하라.

답: 

E(X) = 0, E(X²) = 1.2 이므로 분산 간편식에 의해 var(X) = 1.2 - 02 이다. 

● 흰 달걀 1개와 갈색 달걀 1개가 들어 있는 바구니에서 달걀 2개를 차례로 선택할 때 두 확률 변수 X와 Y를 다음과 같이 정의하자. 

X=1, 첫번째에 흰색 달걀이 나올때 

     0, 첫번째에 갈색 달걀이 나올때 

Y=1, 두번째에 흰색 달걀이 나올때

     0, 두번째에 갈색 달걀이 나올때

X, Y의 결합분포를 (1) 비복원추출일 때 (2) 복원추출일 때 각각 구하라. 

답: 

(1) 비복원 추출의 경우, 조건부 시행이므로

P(X=1, Y=1) = 0

P(X=1, Y=0) = P(Y=0|X=1)P(X=1) = 1/2

P(X=0, Y=1) = P(Y=1|X=0)P(X=0) = 1/2

P(X=0, Y=0) = P(Y=0|X=0)P(X=0) = 0

따라서, 비복원 추출의 경우, X, Y의 결합분포는 다음과 같다. 

(2) 복원추출의 경우는 매 시행이 독립시행이므로 결합분포는 다음과 같다. 

답: 1-α_i 답: 이 실제 i지역에 있을 때 i지역에서 발견할 확률이므로, 우주선이 1지역에 있을 때 1지역에서 발견하지 못할 확률은 1-(1-α₁) = α1 이다. 우주선이 실제 i지역에 있을 사상을 R_i (i=1,2,3)이라고 하고 1지역에서 우주선을 찾지 못할 사상을 N라고 하면 구하고자 하는 조건부확률은 다음과 같다. 

P(R1|N) = P(N∩R1)/P(N) = P(N|R1)P(R1) / ∑P(N|Ri)P(Ri) = (α1x 1/3) /  { α1x 1/3 + 1x1/3 + 1x1/3} = α1 /(α1 + 2)

● 모 상품의 시장 조사 결과는 다음과 같다. 임의의 한 응답자를 선택했을 때 그 사람이  SNS 광고를 시청했을 경우 상품을 구입할 조건부 확률은 얼마인가? 

답: P(상품구입함|SNS광고시청함) = 40/100 = 0.4

● 미국 여성의 10%는 폐암에 걸린다고 한다. 폐암에 걸린 여성 중 80%가 흡연자인 반면 폐암에 걸리지 않은 여성 중 40%가 흡연자라고 한다. 어떤 흡연 여성이 폐암에 걸릴 확률은  몇 %인가? 

답: 베이즈 공식이용

폐암(O) 10% => 흡연 80%  비흡연 20%

폐암(X) 90% => 흡연 40% 비흡연 60%

따라서,  P(폐암|흡연여성)= 0.1x0.8 / (0.1x0.8 + 0.9x0.4) = 0.1818 = 18.18%

● P 대학교 전체 남녀 비율은 여자가 60%이고 여자이면서 머리에 염색을 한 학생의 비율은 30%이다. 여학생 한 명을 선택할 때 그 학생이 머리 염색을 하였을 확률은?

답: 조건부 확률 계산하면 P(염색|여자)=0.3/0.6=0.5

● 코로나 항체 반응검사에서 코로나에 걸린 사람들 중에서 95%가 (+)반응을 보이고 코로나에 걸리지 않은 사람도 1%의 (+)반응을 나타낸다고 한다. 전 국민 중에서 1%의 사람들이 코로나에 감염되었다고 할 때 코로나 반응검사에서 양성반을을 나타낸 사람이 실제로 코로나에 걸렸을 확률은?

답: 베이즈공식 사용하면, 0.01x0.95 / {(0.01x0.95)+(0.99x0.01)} = 0.4896=95/194 

● 어느 지역 주민의 3%가 집단 감염에 걸렸다고 한다. 이 병에 대한 진단방법에 따르면 감염자의 95%가 양성반응을 나머지 5%가 음성반응을 나타내며 비감염자의 10%가 양성반응을 90%가 음성반을을 나타낸다고 한다. 주민 중 한 사람을 임의로 검진한 결과 양성반응을 보였다면 이 사람이 병에 감염되어 있을 확률을 %로 구하시오. 

답: 베이즈 공식 사용, 0.03 x 0.95 / {(0.03x0.95)+(0.97x0.1)} = 22.7%

● 중고 시장에서 거래되는 골동품의 20%가 모조품이라고 알려져 있다. 골동품 감정사들이 진품을 진품으로 평가할 확률은 85%이고, 모조품을 진품으로 감정할 확률은 15%이다. 감정사가 진품이라고 감정한 그림을 어떤 고객이 구매했을 경우, 그 구매한 골동품이 진품일 확률을 구하고 소수 첫째자리까지 %로 나타내시오.

답: 베이즈 공식을 사용하여 95.8%

● 어떤 상자 속에 백색 2개 적색 3개 흑색 5개 모두 10개의 구슬이 들어있다. 이 상자에서 임의로 구슬 3개를 꺼내는 경우, 백색 2개 흑색 1개의 구슬이 나올 확률은?

답: 무작위 비복원추출을 이용하여,  2C2 x 5C1 / 10C3 = 1/24

● L회사의 제품 X에 대한 구매의사를 총 100명(남자 40명 여자 60명)을 상대로 조사하였다. 그 결과 구매의사를 가진 남자는 20% 여자는 50%이었다. 100명 중 임의로 한 사람을 선택했을 경우 여자이면서 구매의사를 가질 확률은?

답: 조건부 확률식을 이용하여 P(구매찬성|여자) = 0.5x0.6 / 0.6= 0.5

● 어떤 나라 국민들 중 왼손잡이의 비율이 남자가 2% 여자가 1%라 한다. 남학생 비율이 60%인 어느 학교에서 왼손잡이 학생을 선택했을 때 이 학생이 남자일 확률은? 

답: 베이즈 공식을 이용하여, 75%

● 나라장터 조사팀은 기상관측기기 X 에 대한 구매의사를 조사하였다. 국가기관40개와 민간 60개 모두 100개 기관을 대상으로 조사한 결과, 구매의사를 보인 기관은 20%, 민간은 50%이었다. 100개 기관 중 임의로 한 기관을 선정하였을 때, 민간인 조건하에서 구매에 찬성할 확률은?

답: P(구매신청 | 민간) = P(구매신청 ∩ 민간) / P(민간) = 0.5 x 0.6 / 0.6 = 0.5

● P(A) =0.3, P(A|B)=0.25, P(Ac∩Bc) = 0.4 일때, P(B|A)는 ?

답:

P(A^c∩B^c) = P(A∪B)^c = 1-P(A∪B)=0.4

P(A|B)=P(A∩B)/P(B) = 0.25이므로, P(A∩B)=0.25P(B)

P(A∪B) = P(A) + P(B) - P(A∩B) = 0.3 + P(B) -0.25P(B) = 0.3 + 0.75P(B) = 0.6 이므로

P(B)=0.4

P(B|A) = P(A∩B)/P(A) = 0.25 x 0.4 / 0.3

1. 전확률 또는 총확률 공식(formula of total probability)

P(Ai) > 0인 사건 A1, A2, …, An을 표본공간 S의 분할이라 하자. 그러면 임의의

사건 B에 대하여 다음이 성립한다.

2. 베이즈 정리 (Bayes’ Theorem)

P(Ai) > 0인 표본공간 S의 분할 A₁, A₂, …, A_n에 대하여, P(B) > 0인 사건 B가 주어졌다는 조건 아래서 사건 Ai 의 조건부 확률은 다음과 같다.

따라서 전확률 공식에 의해 다음을 얻는다. 이 공식을 베이즈 정리라고 한다. 

3. 확률나무

확률나무 이론을 이용하면 베이스 정리 이론을 단순화 시킬 수 있다.

답: 1-αi 답: 이 실제 i지역에 있을 때 i지역에서 발견할 확률이므로, 우주선이 1지역에 있을 때 1지역에서 발견하지 못할 확률은 1-(1-α1) = α1 이다. 우주선이 실제 i지역에 있을 사상을 Ri (i=1,2,3)이라고 하고 1지역에서 우주선을 찾지 못할 사상을 N라고 하면 구하고자 하는 조건부확률은 다음과 같다. 

P(R1|N) = P(N∩R1)/P(N) = P(N|R1)P(R1) / ∑P(N|Ri)P(Ri) = (α1x 1/3) /  { α1x 1/3 + 1x1/3 + 1x1/3} = α1 /(α1 + 2)

2. 모 상품의 시장 조사 결과는 다음과 같다. 임의의 한 응답자를 선택했을 때 그 사람이  SNS 광고를 시청했을 경우 상품을 구입할 조건부 확률은 얼마인가? 

답: P(상품구입함|SNS광고시청함) = 40/100 = 0.4

3. 미국 여성의 10%는 폐암에 걸린다고 한다. 폐암에 걸린 여성 중 80%가 흡연자인 반면 폐암에 걸리지 않은 여성 중 40%가 흡연자라고 한다. 어떤 흡연 여성이 폐암에 걸릴 확률은  몇 %인가? 

답: 베이즈 공식이용

폐암(O) 10% => 흡연 80%  비흡연 20%

폐암(X) 90% => 흡연 40% 비흡연 60%

따라서,  P(폐암|흡연여성)= 0.1x0.8 / (0.1x0.8 + 0.9x0.4) = 0.1818 = 18.18%

4. P 대학교 전체 남녀 비율은 여자가 60%이고 여자이면서 머리에 염색을 한 학생의 비율은 30%이다. 여학생 한 명을 선택할 때 그 학생이 머리 염색을 하였을 확률은?

답: 조건부 확률 계산하면 P(염색|여자)=0.3/0.6=0.5

5.코로나 항체 반응검사에서 코로나에 걸린 사람들 중에서 95%가 (+)반응을 보이고 코로나에 걸리지 않은 사람도 1%의 (+)반응을 나타낸다고 한다. 전 국민 중에서 1%의 사람들이 코로나에 감염되었다고 할 때 코로나 반응검사에서 양성반을을 나타낸 사람이 실제로 코로나에 걸렸을 확률은?

답: 베이즈공식 사용하면, 0.01x0.95 / {(0.01x0.95)+(0.99x0.01)} = 0.4896=95/194 

6. 어느 지역 주민의 3%가 집단 감염에 걸렸다고 한다. 이 병에 대한 진단방법에 따르면 감염자의 95%가 양성반응을 나머지 5%가 음성반응을 나타내며 비감염자의 10%가 양성반응을 90%가 음성반을을 나타낸다고 한다. 주민 중 한 사람을 임의로 검진한 결과 양성반응을 보였다면 이 사람이 병에 감염되어 있을 확률을 %로 구하시오. 

답: 베이즈 공식 사용, 0.03 x 0.95 / {(0.03x0.95)+(0.97x0.1)} = 22.7%

7. 중고 시장에서 거래되는 골동품의 20%가 모조품이라고 알려져 있다. 골동품 감정사들이 진품을 진품으로 평가할 확률은 85%이고, 모조품을 진품으로 감정할 확률은 15%이다. 감정사가 진품이라고 감정한 그림을 어떤 고객이 구매했을 경우, 그 구매한 골동품이 진품일 확률을 구하고 소수 첫째자리까지 %로 나타내시오.

답: 베이즈 공식을 사용하여 95.8%

8. 어떤 상자 속에 백색 2개 적색 3개 흑색 5개 모두 10개의 구슬이 들어있다. 이 상자에서 임의로 구슬 3개를 꺼내는 경우, 백색 2개 흑색 1개의 구슬이 나올 확률은?

답: 무작위 비복원추출을 이용하여,  2C2 x 5C1 / 10C3 = 1/24

9. L회사의 제품 X에 대한 구매의사를 총 100명(남자 40명 여자 60명)을 상대로 조사하였다. 그 결과 구매의사를 가진 남자는 20% 여자는 50%이었다. 100명 중 임의로 한 사람을 선택했을 경우 여자이면서 구매의사를 가질 확률은?

답: 조건부 확률식을 이용하여 P(구매찬성|여자) = 0.5x0.6 / 0.6= 0.5

10. 어떤 나라 국민들 중 왼손잡이의 비율이 남자가 2% 여자가 1%라 한다. 남학생 비율이 60%인 어느 학교에서 왼손잡이 학생을 선택했을 때 이 학생이 남자일 확률은? 

답: 베이즈 공식을 이용하여, 75%

11. 나라장터 조사팀은 기상관측기기 X 에 대한 구매의사를 조사하였다. 국가기관40개와 민간 60개 모두 100개 기관을 대상으로 조사한 결과, 구매의사를 보인 기관은 20%, 민간은 50%이었다. 100개 기관 중 임의로 한 기관을 선정하였을 때, 민간인 조건하에서 구매에 찬성할 확률은?

답: P(구매신청 | 민간) = P(구매신청 ∩ 민간) / P(민간) = 0.5 x 0.6 / 0.6 = 0.5

12. P(A) =0.3, P(A|B)=0.25, P(Ac∩Bc) = 0.4 일때, P(B|A)는 ?

답:

P(Ac∩Bc) = P(A∪B)c = 1-P(A∪B)=0.4

P(A|B)=P(A∩B)/P(B) = 0.25이므로, P(A∩B)=0.25P(B)

P(A∪B) = P(A) + P(B) - P(A∩B) = 0.3 + P(B) -0.25P(B) = 0.3 + 0.75P(B) = 0.6 이므로

P(B)=0.4

P(B|A) = P(A∩B)/P(A) = 0.25 x 0.4 / 0.3

1. 조건부 확률

 어떤 사건 B가 일어났다는 조건하에 (또는 정보 B를 안다는 가정하에서) 사건 A의 확률을 생각할 때, 그 확률을 A의 조건부 확률(conditional probability) 이라 부르고 P(A|B)로 표현한다. 계산식은 아래와 같다.

2. 독립 사상

3. 승법정리(multiplicative rule) 또는 곱의 규칙

조건부 확률의 응용으로서 곱사건의 확률공식인 승법정리를 얻을 수 있다.

4. 독립 사건

독립 사건(independent events): P(A) > 0 또는 P(B) > 0일 때 사건 A의 발생여부가 사건 B의 발생에 영향을 미치지 않는 경우, 즉 다음을 만족하는 두 사건을 독립이라 한다.

P(A|B) = P(A)  또는  P(B|A) = P(B)

 

 

● 미국 NASCAR 자동차 경주에서 A가 이길 확률이 1/7, B는 A의 2배, C는 B의 2배일 때, C가 이길 확률은?

답: 1/7 x 2 x 2 = 4/7

● 파란구슬 5개, 빨간구슬 4개 노란구슬 3개가 들어있는 상자가 있다. 이 구슬들 중에서 임의로 1개의 구슬을 꺼낼 때 빨간구슬일 확률은?

답: 4C1/12C1 = 4/12= 1/3

● 모조품 4개와 진품 3개가 섞여 있는 상자에서 2개의 제품을 비복원으로 추출할 때, 모조품이 적어도 1개일 확률은?

답: 여확률을 사용하여, 1-(3C2/7C2) = 1-1/7 = 6/7

● 사상 A와 B가 발생할 확률이 각각 0.5, 0.6이라고 하자. A또는 B가 발생할 확률이 0.8일 때, 사상 A와 B가 동시에 일어날 확률은?

답: 교사건 확률을 구하면 P(A∩B)=P(A)+P(B)-P(A∪B)=0.5+0.6-0.8= 0.3

● 어떤 상자 속에 백색 2개 적색 3개 흑색 5개 모두 10개의 구슬이 들어있다. 이 상자에서 임의로 구슬 3개를 꺼내는 경우, 백색 2개 흑색 1개의 구슬이 나올 확률은?

답: 무작위 비복원추출을 이용하여,  2C2 x 5C1 / 10C3 = 1/24

1. 확률의 정의 

주관적 확률(subjective probability) : 주어진 사건의 발생 가능성(즉, 확률)을 분석자의 경험과 지혜에 의해 정하는 과정

상대도수 확률(probability as a relative frequency) : 어떤 사건의 확률을 상대도수로서 정하는 방법

등확률 모형으로부터의 확률

: 등확률 모형이라는 수학적 모델로부터 확률을 정하는 방법

표본공간  S 의 원소가 n개일 때 등확률 모형에서는 n개의 근원사건이 일어날 확률이 모두 1/n 이라고 가정

통계적 확률

시행을 n번 반복하여 사건 A가 일어난 횟수를 rn  이라 할때, n 을 한없이 크게함에 따라 상대도수 rn/n  이 일정한 값 p에 가까워지면 p를 사건 A의 통계적 확률이라고 한다.

영역 S에서 임의로 잡은 점이 영역 A에 속할 확률

공리적 확률 (axiomatic probability)

2. 확률의 성질

확률의 단조성

어느 도시의 오전 10시 평균 기온을 구하기 위하여 5개 기상관측소를 무작위로 선택하여 아래 자료를 추출하였다. 아래 물음에 답하시오. 측정한 섭씨기온 (X_i)와 화씨기온(Y_i) 사이에 Y_i = 9/5 X_i + 32 라는 관계가 있다. 

(1)  Y_i의 산술 평균을 구하시오. 

답: 37.4 ℉

(2) Y_i의 표본분산을 구하시오. 

답: 4.86 ℉