728x90
반응형
기대값의 성질
E(X) = μ
E(a X) = a E(X), 단 a는 상수
E(X + b) = E(X) + b, 단 b는 상수
E(X + Y) = E(X) + E(Y)
E[(ab(X) + cd(Y)] = a E[b(X)] + c E[d(Y)], 단 a, c는 상수
E(ab XY) = ab E(XY), 단 a,b는 상수 (만약, 독립이면 E(ab XY) = ab E(X) E(Y) )
분산의 성질
Var(X) = E[(X-μ)2] = E(X2) - [E(X)]2
Var(a) = 0, 단 a는 상수
Var(aX) = a2 Var(X), 단 a는 상수
Var(a + b X) = b2 Var(X), 단 a와 b는 상수
Var(aX + bY) = a2 Var(X) + b2 Var(Y) + 2ab Cov(X,Y), 단 a와 b는 상수
Var(aX - bY) = a2 Var(X) + b2 Var(Y) - 2ab Cov(X,Y), 단 a와 b는 상수 (만약, 독립이면 Cov(X,Y)=0)
1. 이산형 분포의 기댓값
확률변수 X의 치역이 R이고 이산형 분포를 갖는다고 가정하자.
이때 다음이 성립하면 확률변수 X는 기댓값이 존재한다.

다음 값을 X의 기댓값(expectation)이라 한다.


어느 복권의 상금을 확률변수 X로 하여 다음과같은 확률분포를 생각해 보자.


확률변수의 기대값

X의 분포로부터 직접 기댓값을 구하는 경우


2. 기대값의 성질

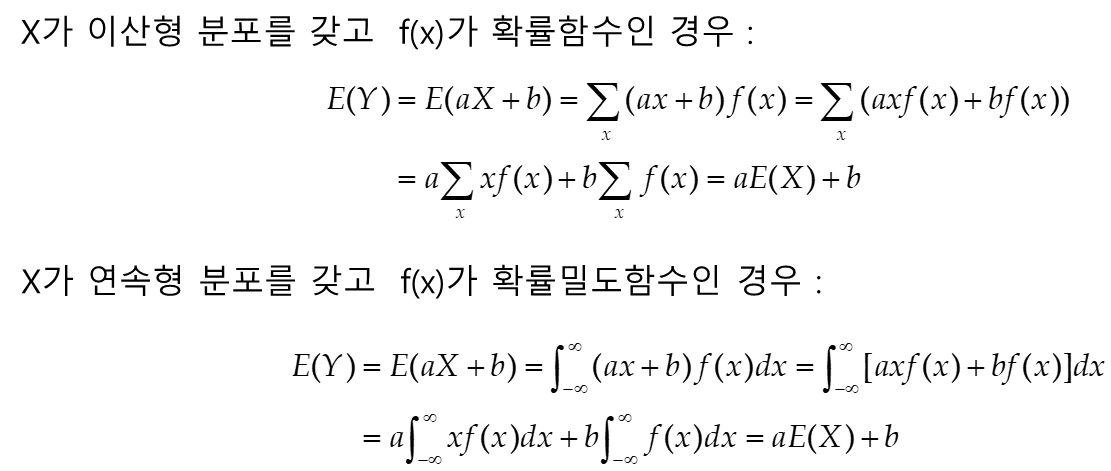


3. 분산


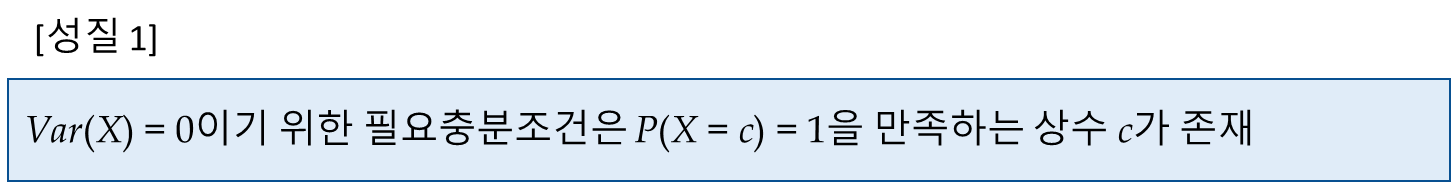



728x90
반응형