기상 기후 강의 노트

3개의 방정식  하나로 표기하는 방법

들어가기 전에 1

들어가기 전에 2 (수리물리 교재 정리)

https://aeir.tistory.com/entry/TKE-%EC%9C%A0%EB%8F%84

플럭스

단위시간당 단위면적당 어떤 양의 이동 (유량)

경계층 기상학에서는 주로 mass, heat, moisture, momentum, pollutant flux 를 고려함. 

아래는 각 플럭스와 SI Unit.

기온, 바람과 다리 열, 운동량은 직접 측정할 수 없다.

따라서, 습윤공기 밀도로 나누어 아래와 같이 운동학적 플럭스를 사용하는 것이 측정을 위해서 편리함.

운동학적 플럭스 (Kinematic flux)

각각의 플럭스는 아래와 같이 3방향 요소를 가진다. 

에디 플럭스 (Eddy flux)

난류의 생성, 억제, 소멸 

난류의 생성: 열적 (부력) 상승과 기계적 에디에 의해서

난류의 억제: 정적 안정 감율에 의해서

난류의 소멸: 분자 점성효과에 의해서 열로 전환됨.

난류 운동 에너지 Turbulence Kinetic Energy

운동 에너지 (KE) = 0.5 m V^2   (여기서, m 은 질량; V은 속도)

유체역학에서는 편리를 위해서 단위 질량에 대해서만 논하므로, KE = 0.5 V^2

TKE는 평균류 부분(MKE/m)와 난류 부분(TKE)로 나눌 수 있다. 

레이놀즈 분해를 적용하면 아래와 같이 표현된다. 

e : 단위 질량 당 순간적인 난류 운동 에너지

e 를 특정 시간에 대해서 평균하면 아래와 같다. 

TKE는 경계층 기상학에서 매우 중요

TKE의 생성 항 vs. 소멸 항 에 의해서 난류가 발달할지 소멸될지가 결정됨. 

아래 그림은 전형적인 TKE의 일변화

여러가지 경계층 조건에 따른 연직 TKE 프로파일

응력 (Stress)

물체의 변형을 일으킬 수 있는 힘. 

단위: F/A

대기과학에서 자주 나오는 3가지 응력: 압력, 레이놀즈 응력, 점성 전단 응력 

유한소의 유체 요소(부피, cube)를 도입하여 이해한다.

1. 압력 (Pressure)

압력: 정적인 상태의 유체에 작용하는 응력

압력은 물체의 모든 방향에 동일하게 작용한다 (isotropic)

방향에 독립이다. 

압축과 팽창으로 물체를 변형시킨다

스칼라

1 Pa = 1 N/m^2

100 Pa = 1 mb

표준대기압 = 1.013 x 10^5 N/m^2 at sea level

정역학 근사 (hydrostatic approximation)로 표현되는 것 처럼 아래 다른 응력보다 크다.

2. Reynolds stress (레이놀즈 응력)

레이놀즈 응력: 유체가 난류 운동을 할 때만 존재한다. 

Fig (d) 난류 에디는 풍속차에 의해서 발생한다. 유한소의 한 면에서 난류 에디는 공기를 유한소 방향으로 수송할 수 있다.  이때, 수송되는 비율을 운동량 플럭스 (momentum flux) 라고 한다. 따라서, 레이놀즈 응력=운동량 플럭스

Fig (e) 유한소의 한 면에만 에디가 작용한다고 가정하면, 반대면에서의 속도차이에 의해 유한소는 변형된다. 

따라서, 난류 운동량 플럭스는 응력(stress) 과 같고 이 것을 Reynold stress 라고 한다. 

예를 들어, 상방으로 움직이는 공기 (w' >0)는 유한소 방향(negative x 방향)으로 u'비율로 혼합되고, 결과적으로 레이놀즈 응력과 운동량 플럭스의 크기(운동학적 단위: 밀도로 나눔)는 각각 아래와 같다. 

Fig (f) 유한소의 한 면만 고려할때, 어떤 방향으로도 움직이는 공기는 유한소 방향으로 이동하여 혼합되어 유한소의 변형이 발생한다. 따라서, 유한소의 한면에 대해서 아래 3개의 요소를 고려해야 한다. 

유한소의 3면에 대해서 모두 고려하면, momemtum flux와 같이 총 9개의 레이놀즈 응력의 요소를 가지게 된다. 

3. 점성 (전단) 응력 (Viscous Shear Stress)

점성 전단 응력은 유체 내 전단 운동이 있을 때만 존재한다.

유체의 일부가 움직이면, 분자 간의 힘에 의해서 가까이 있는 유체를 동일 방향으로 끌어당긴다. 

점성력은 유한소의 3면 중 어느 방향으로도 작용한다. 

점성 응력이 전단력과 선형적인 관계를 가지는 유체를 Newtonian fluid 라 부른다. 

4. 마찰 속도

지표면 근처에서 바람 쉬어에 의해 난류가 발생하는 경우, 지표 레이놀즈 응력의 크기는 중요. 

지표면 근처에서 측정되는 총 수평 운동량의 연직 플럭스는 아래와 같다. 

위 관계를 기초로 마찰속도(u_*)는 아래와 같이 정의된다. 

https://truman.tistory.com/88

http://melonicedlatte.com/2021/03/14/181700.html

아래 조건의 경우, 아래 값들을 구하시오. 

난류 강도

상관계수

난류운동에너지 (Turbulence Kinetic Energy)

해설:

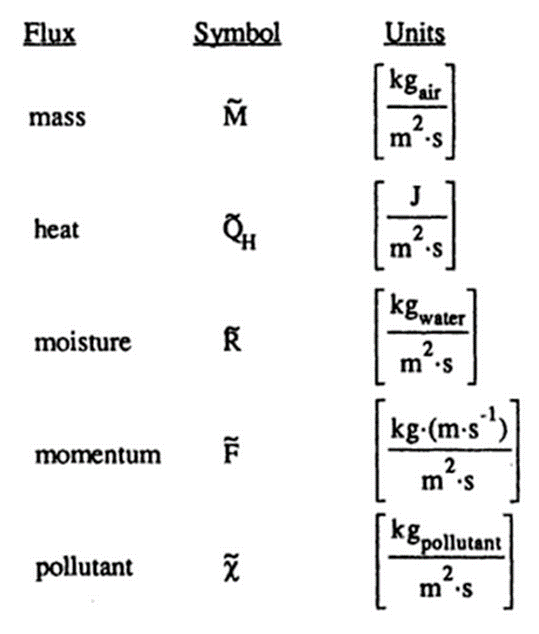
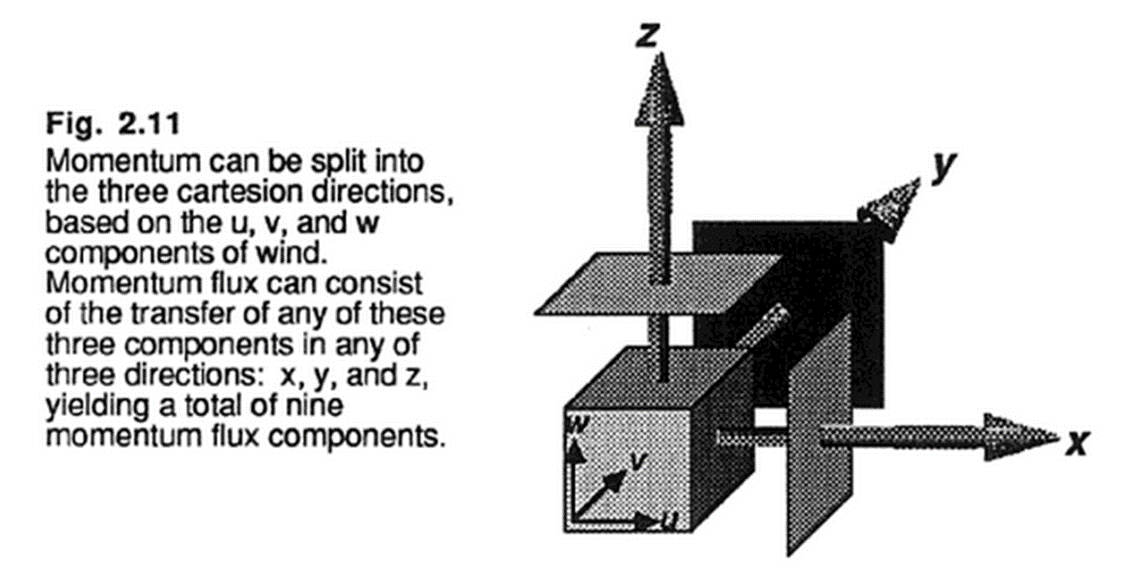
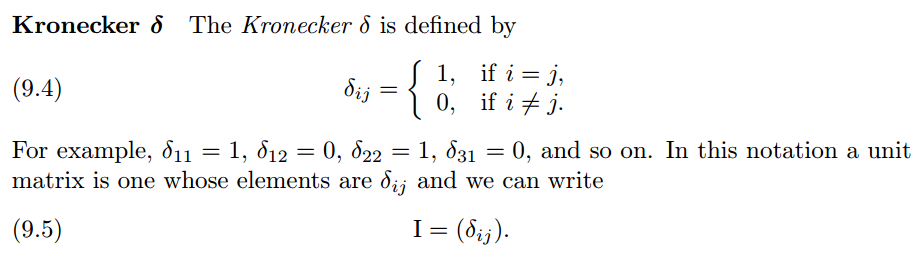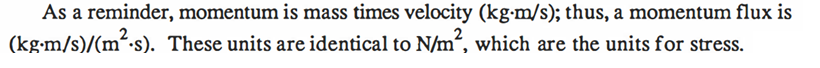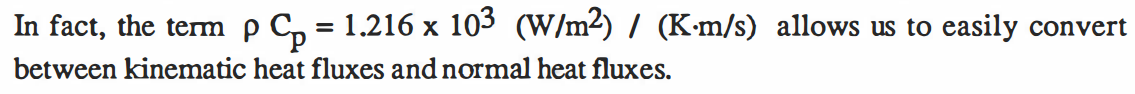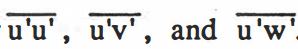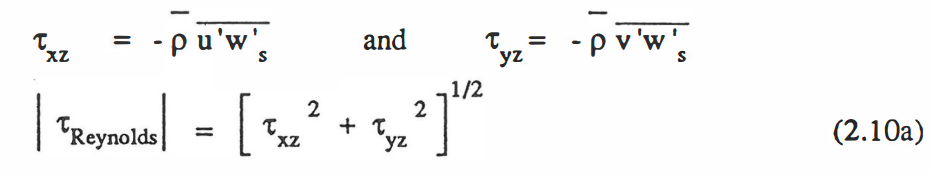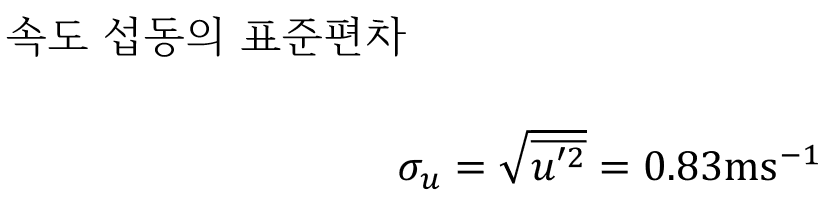유체점성 (fluid viscosity):

분자 특성으로서 유체 내부에서 변형에 대한 저항의 측정치

모든 유체(액체, 기체)는 점성을 가지고 있다.

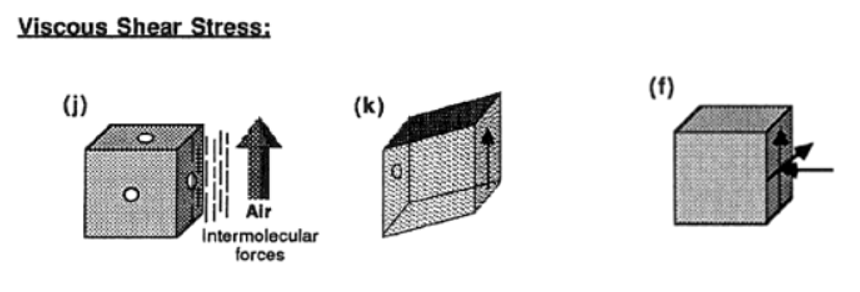
점성효과1: 인접한 유체층 사이의 마찰저항의 요인이 된다.

인접한 유체층 사이의 마찰저항의 요인이 되고, 층밀림응력으로 나타난다. 

단위면적당 저항력은 층밀림 운동(shearing motion)과 관련있기 때문에, 층밀림 응력 (shearing stress)라고 부른다.

층밀림 응력의 예는 아래 링크의 그림 참조

https://ko.wikipedia.org/wiki/%EC%A0%84%EB%8B%A8_(%EB%AC%BC%EB%A6%AC) 

고정면에서 높이(h)까지 유체 속도는 선형적으로 변하기 때문에, 흐름 내 어디서나 속도경도는 아래와 같다. 

∂u/∂z=U/h

뉴턴은 이 흐름을 층밀림 응력(shearing stress)이 응변율(rate of strain; 즉 속도경도율)에 비례한다는 것을 발견하여 아래 식을 제시하였다. 

  τ=μ(∂u/∂z)

• τ: 층밀림 응력
• μ: 점성계수, 즉 유체의 역학적 점성 (dynamic viscosity). 동점성 (mechanical viscosity) ν=μ/ρ 를 사용하는 것이 더 편리, 차원은 L² T^-1 

실제 유체는 위 그림과 같이 1차원방향이 아닌 3차원방향에 대해서 변동하므로, 일반적인 관계식은 아래와 같다.

  τ_xy =   τ_yx = μ(∂u/∂y + ∂v/∂x)

  τ_xz =   τ_zx = μ(∂u/∂z + ∂w/∂x)

  τ_yz =   τ_zy = μ(∂v/∂z + ∂w/∂y)

• 첫째 첨자: 층밀림 응력이 작용하는 면의 수직인 방향
• 둘째 첨자: 응력의 방향.

이 식의 의미: 뉴턴 유체에서는 ‘층밀림 응력은 응변율 (또는 우변의 괄호 항)에 비례한다’는 것. 응력과 변형 모두 흐름 내 한 점, 한 순간 양이다.

점성효과2: 유체 운동 에너지의 소멸.

유체가 운동을 유지하려면 운동 에너지는 외부에서 지속 공급되거나, 위치에너지(압력 또는 밀도경도)로 부터 전환되어야 한다. 점성은 유체 운동 에너지를 열로 전환하면서 소명시킨다. 

점성흐름의 예

경계층, 혼합층, 제트류, 플룸(plume), 꼬리흐름(wake)

층류와 난류 흐름

층류:

인접층이 서로 미끄러지기 때문에 층을 횡단하는혼합과 이동은 거의 없다. 비점성흐름은 층류와는 달리 층 간의 운동량, 열, 질량의 이동이 발생.

난류:

불규칙, 무작위, 3차원형태이고, 확산(혼합)적인 운동이다. 대부분의 흐름은 난류. But, 3차원 소규모 난류. 2차원 (대규모) 난류는 구별해야!!

시/공간의함수로서 정확히 계산/예측될 수 없다. 따라서 난류의 평균적인 통계 특성을 다룰수 밖에 없다.

레이놀즈 평균과 분산 

대기권에서의 층류 발생은 극히 드물고, 보통 점성아층 (viscous sublayer, 예. 얼음, 진흙평면, 잔잔한 수면) 등에서만 다룬다.

용어정리

• 점성 아층: 완전 층류는 아니고, 약간의 점성이 고려되기는 해도 점성 흐림이라 보기에는 애매한 경계(인접한) 층.  분자 아층과 같은 말. )
• 아층 (Sublayer; 또는 부층). 표면에 인접한 얇은 층 영역. 비슷한 말: 아지표 (subsurface):  지표에 인접한 영역
• 분자 아층 (molecular sublayer): 경계면 (interface) 인접 부근, 즉 분자 아층 (molecular sublayer; <1 mm) 내에서는 공기의 주된 열 전달 방법인 전도(conduction)로서 고체와 같다. 경계면에서 수 mm 만 올라가도 공기의 주된 열 전달 방법은 이류(advection)과 대류(convection)이다.  호수나 해양에서 분자 아층은 수 m 이다.

scp -r ./data/GDAS/201601 {username}@XXX.XXX.XXX.103:/data/GDAS

지구는 아래 어떤 시기에 태양과 가장 가까운가?

• 북반구 겨울
• 남반구 봄
• 남반구 가을
• 남반구 겨울

계절이 생기는 근본적인 원인은 무엇인가?

• 황도면에 대해 기울어진 지구자전 궤도
• 태양방출 에너지의 연간 변화
• 지구의 타원궤도
• 매일 변하는 날씨
• 지구와 태양의 거리

슈테판-볼쯔만의 법칙은 무엇과 무엇의 관계를 설명하는 것인가?

가시광선이 사물에 부딪혀 반사되는 비율을 무엇이라고 부르나 ?

• 알베도
• 보웬비
• 잠열
• 산란
• 방출률

하층 대기에서 가장 중요한 흡수 기체 두 가지는 무엇인가?

온실효과는 다음의 어떤 현상을 의미하는가?