기상 기후 강의 노트

앙상블 방법

분류에서 가장 각광 받는 방법

이미지, 영상, 음성,NLP  영역에서 신경망ㅌㅊ에 기반한 딥러닝이 머신러닝계를 선도하고 있지만, 이를 제외한 정형 데이터의 예측 분석 영역에서는 앙상블ㅇ리 매우 높은 예측 성능으로 애용되고 있음. 

앗으븡:

서로 다른/또는 같은 알고리즘을 단순히 결하한 형태이나, 일반적으로 배팅과 부스팅 방식으로 나눔.

배깅방식: 랜덤 포레스트 - 뛰어나난 예측 선응 상대적으로 빠른 수행 시간, 유연성

최근에는 부스팅 방식으로 발전하고 있음. 그래디언트 부스팅(효쇠) 뛰어난 예측 성능이지만, 시간이 너무 오래 걸림따라서 최적화 모델 튜닝이 어려움

XgBoost , lightGBM 등 기존 그래디언트 부스팅의 예측 성능을 한단계 발전시키ㅁ녀서 수행시간을 단축시킨 알고리즘

정형 데이터 분류 영여ㅓㄱ에서 가장 활용도가 높으 ㄴ알고리즘으로 자리 잡음

랜덤 포레스트

그래디언트 부스닝

XGboost LightGMBM 스태킹 기법에 대해ㅓㅅ 살료봄. 

앙상블의 기본 알고리즘 --> 결정트리

결정트리: 쉽고 유연

스케일링이나 정규화 등의 영향이 적다. 

복잡한 구조로 인한 과적합이 발생하여 예측 성능이 저하될 수도 있음. 

하지마나 이것이 오ㄹ히려 장점

왜냐하면, 앙상블은 매우 많은 여러개의 약한 학습기(예측 성능이 상대적으로 낮은 학습 알고리즘)를 결합해 확률적 보와노가 유로가 발생한 부분에 대한 가중치를 계속 업데티으하면서 옟윽 성능을 향상시키는데 결정 트리가 좋은 약한 학습기가다 되기때문

결정트리

앙상블 학습

랜덤 포레스트

GBM

XGBoost

LightGBM

캐글 산탄데르 고객 만족 예측

출처: 파이썬 머신러닝 완벽가이드

신경망 구조

1. 네트워크(또는 모델)를 구성하는 층

2. 입력 데이터와 그에 대응하는 타깃

3. 손실함수: 예측과 타깃을 비교하여 모델의 예측이 기대값에 얼마나 잘 맞는지 측정하는 손실값을 만듬

4. 학습 진행방식을 결정하는 옵티마이저

모델: 

층의 네트워크

딱 맞는 네트워크 구조를 찾는 것은 과학보다 예술. 연습 필요.

>>> from keras import models

>>> from keras import layers

>>> model = model.Sequential() 

Sequential() 모델의 경우, 단일 입력, 단일 출력인 경우 사용

다중입력 데이터 + 여러 딥러닝 모듈 인 경우 함수형 API 사용

모델 설정 - 층 설정

입력층, 은닉층, 출력층 등의 딥러닝의 구성 단위

하나 이상의 텐서를 입력받아 하나 이상의 텐서를 출력하는 데이터 처리 모듈

가중치: 대부분의 층은 가중치를 가짐. 네트워크(모델)가 학습한 지식이 가중치에 담겨 있음. 

>>> model.add(layers.Dense(32, input_shape=(784,)) activation = 'relu')

첫번째 차원이 784인 2D텐서만 입력으로 받는 층을 만듬.

배치 차원인 0번째 축은 지정하지 않았기 때문에 어떤 배치 크기도 입력받을 수 있음

이 층은 첫번째 차원 크기가 32로 변환된 텐서를 출력함

즉, 이 다음 하위층은 32차원의 벡터를 입력으로 받는 하위 층으로 연결되어야 함. 

(Kerase에서는 자동으로 층 호환성을 맞춤)

>>> model.add(layers.Dense(10), activation='softmax')

input_shape을 지정하지 않아도 Kerase에서는 자동으로 앞선 층의 출력크기로 맞춰줌.

컴파일 - 손실함수와 옵티마이저: 학습 과정을 조절하는 열쇠!

>>> from keras import optimizers

>>>model.comopile(optimizer = optimizers.RMSprop(r=0.001), 

... loss='mse'

... metrics=['accuracy'])

손실(또는 목적)함수:

모델의 최적 매개변수(가중치, 편향) 학습에 필요한 에러 측정 함수

네트워크(망)이 예측한 결과와 데이터 세트에 명시된 실제 결과의 차이를 측정

훈련하는 동안 최소화될 값. 주어진 문제에 대한 성공 지표

손실함수 정의 방법: 

분류문제: 데이터 세트의 데이터 중 잘못 분류한 비율을 계산하고, 그 비율을 에러 발생 확률로 사용

회귀문제: 입력 데이터로 예측한 결과와 실제 결과 간의 차이를 계산하여 평균을 구함.

옵티마이저 - 손실함수 최적화

손실 함수를 기반으로 네트워크가 어떻게 업그레이드 될 지 결정. 확률적 경사 하강법 사용해서 구함. 

여러개의 출력을 만드는 신경망은 또한 여러 개(vector or tensor)의 손실함수를 가질 수 있음 (출력당 하나씩).

경사 하강법은 하나의 손실값(scalar)을 이용하기 때문에, 모든 네트워크에서 출력된 손실의 평균값을 계산.

신경망은 단지 손실함수를 최소화하기만 한다. 따라서, 목적 함수를 올바로 선택하지 않으면 원치않는 side effects가 커질 수 있다.

올바른 손실/목적함수 선택법:

1. binary_crossentropy (이항 교차 엔트로피 또는 이진 크로스엔트로피): 이진 분류 문제. 참/거짓 2개의 클래스를 분류할 때

2. categorical_crossentropy 범주형 크로스엔트로피: 여러개의 클래스 분류할 때

3. mean_squared_error 평균 제곱 오차: 회귀문제

4. mean_absolute_error 평균 절대 오차: 회귀문제

5. mean_absolute_percentage_error: 평균 절대 백분율 오차: 회귀문제

6. CTC(Connection Temporal Classification): 시퀀스 학습 문제

모델 실행 - 모델링 (fitting)

>>> model.fit(X, Y, epochs=100, batch_size=10)

일반적인 데이터 셋 csv 파일의 경우, 가로행(속성 또는 피쳐 feature), 세로열(샘플 또는 인스턴스instance 또는 example))로 구성됨. 

Epochs

학습 프로세서가 모든 샘플 에 대해 한 번 실행되는 것을 1epoch

epochs=100 이면, 각 샘플이 처음부터 끝까지 100번 재사용될 때가지 실행을 반복하라는 뜻. 

batch_size:

샘플을 한번에 몇개씩 처리할지 정하는 부분

batch_size=10 이면 전체 샘플 중 10개씩 끊어저 집어넣으라는 뜻.

너무 크면 학습도 저하, 너무 작으면 편차가 높아져 결과값이 불안정해 짐

따라서, 현재 시스템의 메모리가 감당할 만큼의 batch_size를 찾아 설정해 주는 게 관권. 

모델평가 

학습/테스트 세트로 구분하여 평가

과소적합/과적합

MNIST 손글씨 딥러닝 예제를 통한 신경망 구조 설명

1. 훈련/테스트 세트 구성

>>> import tensorflow as tf  

>>> from kerase.datasets import mnist
>>>  mnist = tf.keras.datasets.mnist
>>> (x_train, y_train), (x_test, y_test) = mnist.load_data()  # train / test set을 알아서 나눔
# mnist 데이터는 0~255 범위의 데이터 
# 이를 0~1 사이로 맞춰주기 위해서 255로 나눔.
# 딥러닝은 0~1 사이로 input 데이터의 범위를 해줘야.

>>> x_train, x_test = x_train / 255.0, x_test / 255.0
>>> x_train.shape

2. 모델 구성

Layer(층):

데이터 처리 필터 

어떤 데이터가 들어가면 더 유용한 형태로 출력됨.

즉, 주어진 문제에 더 의미 있는 표현을 입력 데이터로 부터 추출함

여러 층을 통과하면서 점진적으로 데이터를 정제함.

데이터 정체 필터(층)가 연속되어 있는 데이터 프로세싱을 위한 여과기 같다고 생각할 수 있음. 

>>> model = tf.keras.models.Sequential([
...  tf.keras.layers.Reshape((28, 28, 1)),
...  tf.keras.layers.Conv2D(16, 3, activation='relu'),
...  tf.keras.layers.Flatten(),
...  tf.keras.layers.Dense(128),
...  tf.keras.layers.Dense(10, activation='softmax')
... ])

3. 컴파일 (compile)

손실함수 (loss function):

신경망의 성능을 측정하는 방법

모델(네트워크)이 옳은 방향으로 학습될 수 있도록 해줌. 

옵티마이저(optimizer):

입력 데이터와 손실 함수를 기반으로 네트워크를 업데이트하는 메커니즘

모니터링 지표

정확도 등

>>> model.compile(optimizer='adam',
...              loss='sparse_categorical_crossentropy',
...              metrics=['accuracy'])

4. 학습

>>> model.fit(x_train, y_train, epochs=5)

5. 모델 평가

>>> test_loss, test_acc = model.evaluate(x_test, y_test)
>>> print('테스트 정확도:', test_acc)

구글 플레이그라운드에 접속

https://playground.tensorflow.org 

1. 문제유형 선택 (먼저, 선형 분리되는 작업 선택)

2. 훈련/테스트 데이터 비율 설정

3. 입력 특징 선택

4. 학습율 설정: 학습속도 결정

5. 활성화함수 선택

6. 학습시작

7.  선형분리 안되는 작업에 은닉층 추가해서 실행해서 분류 도표 차이 보기

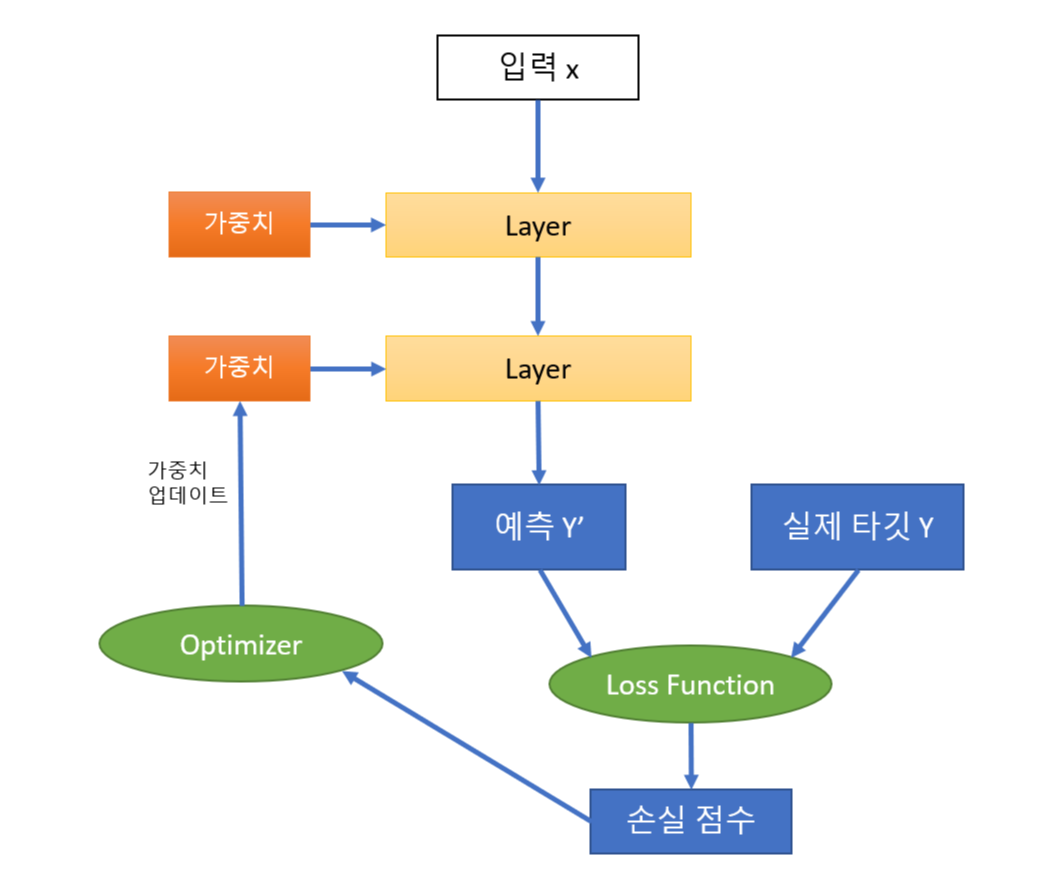
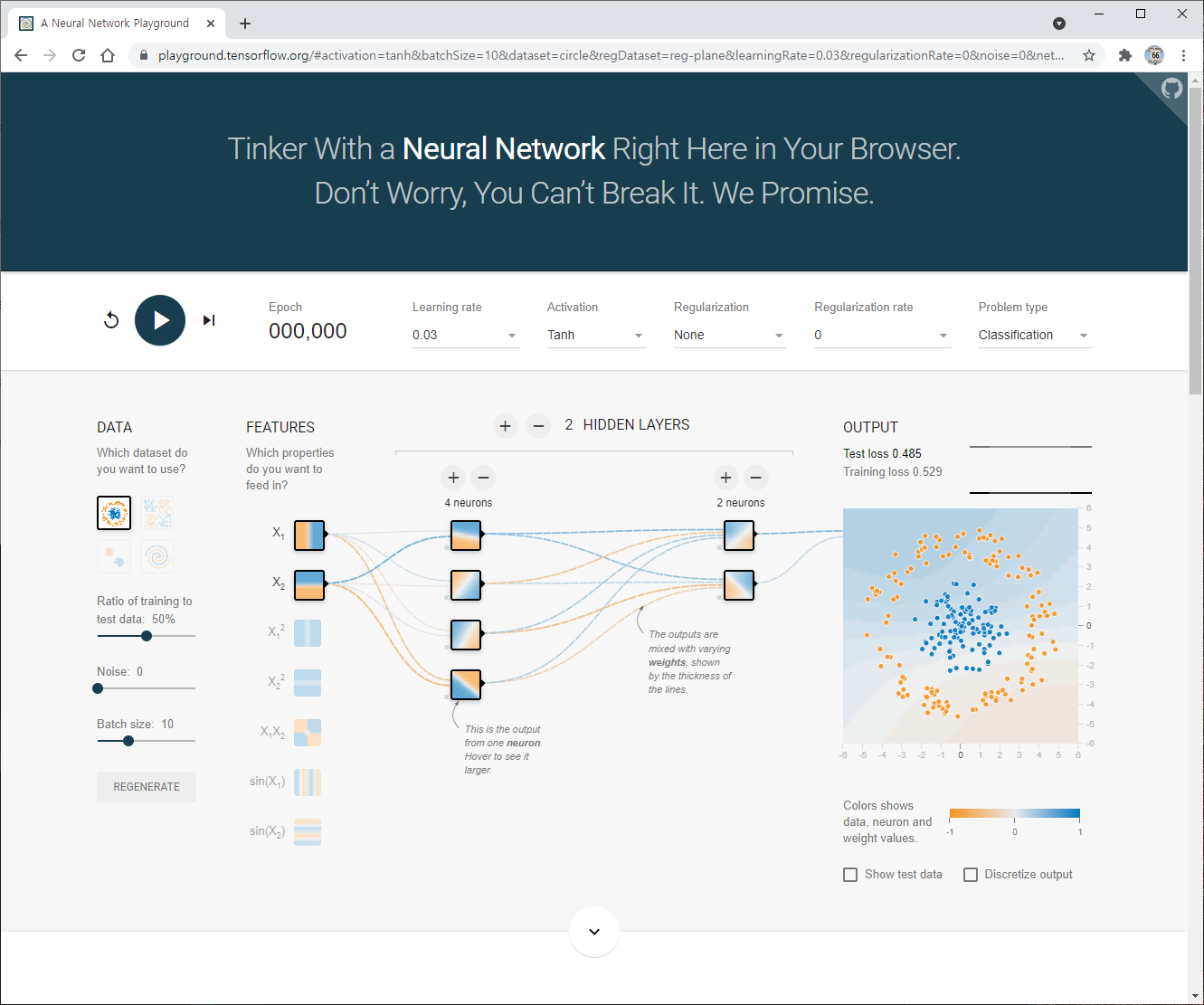
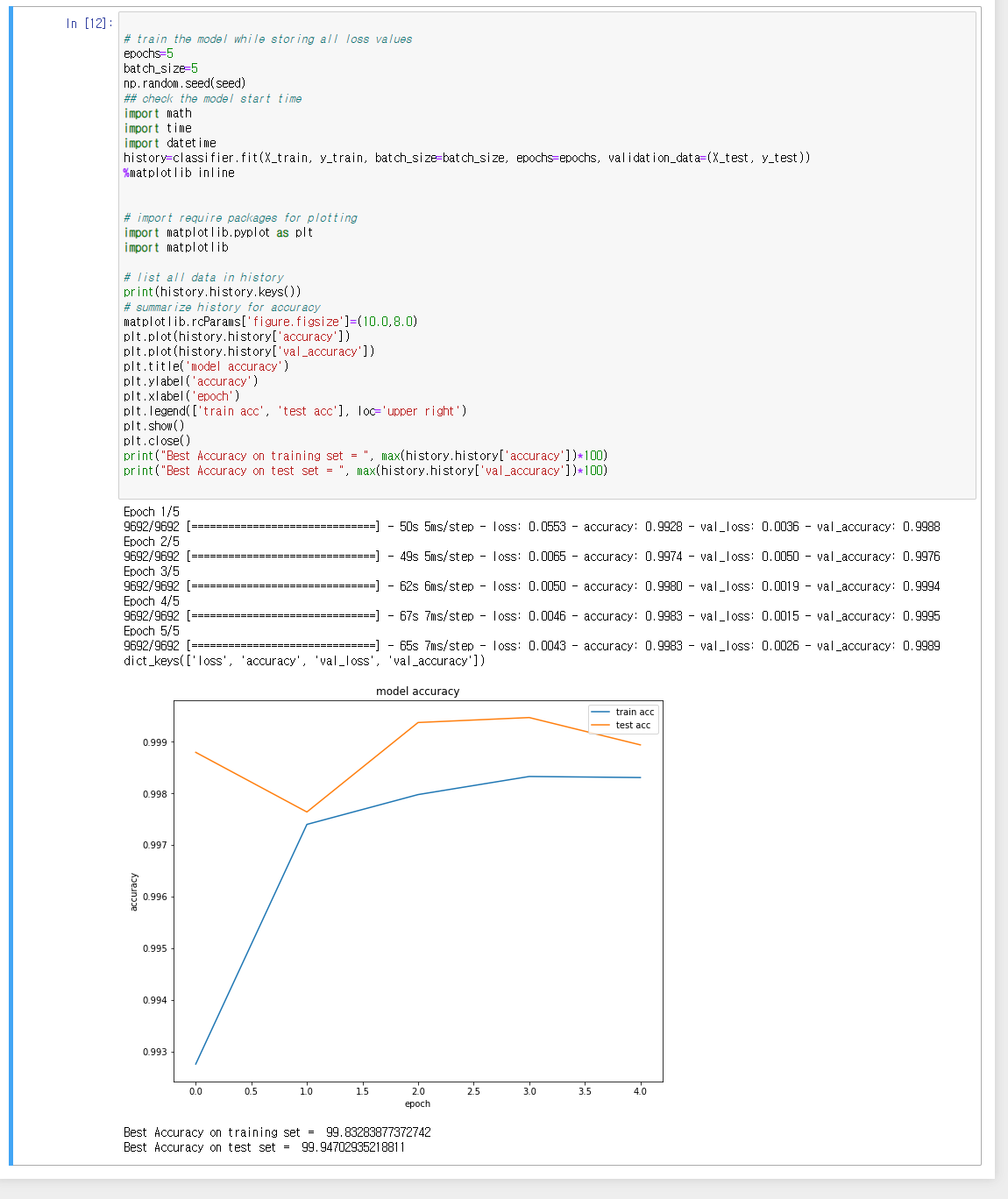
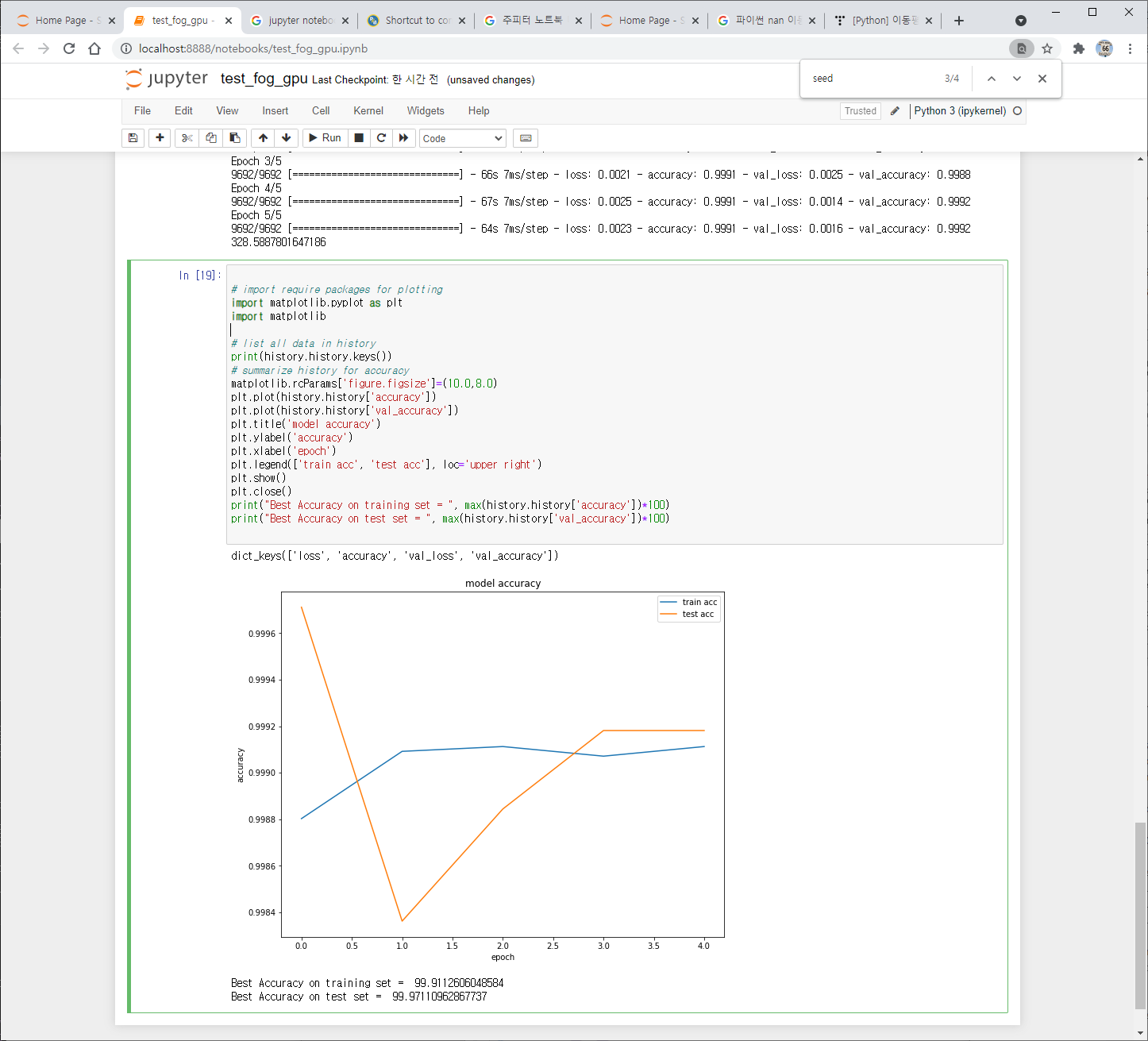
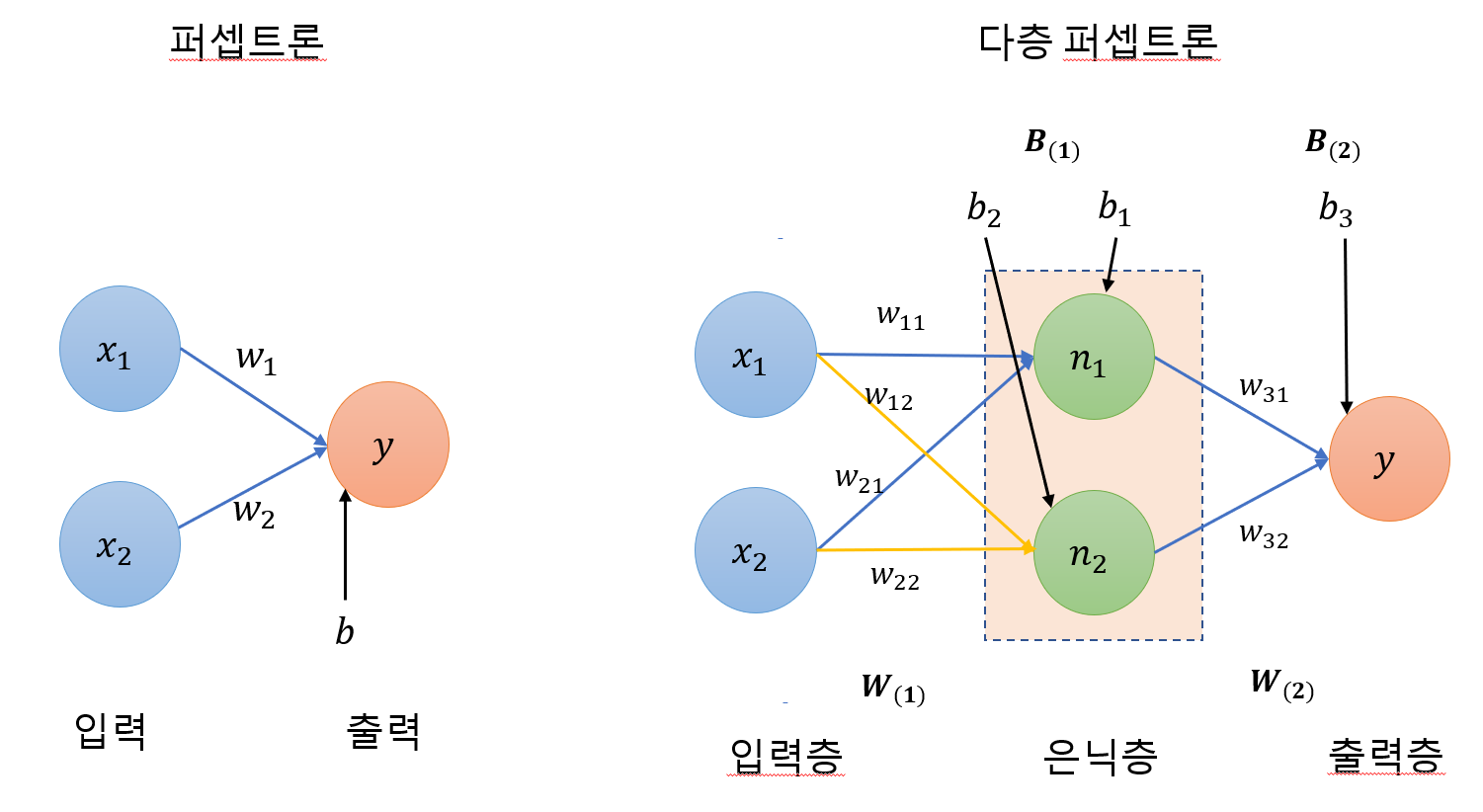
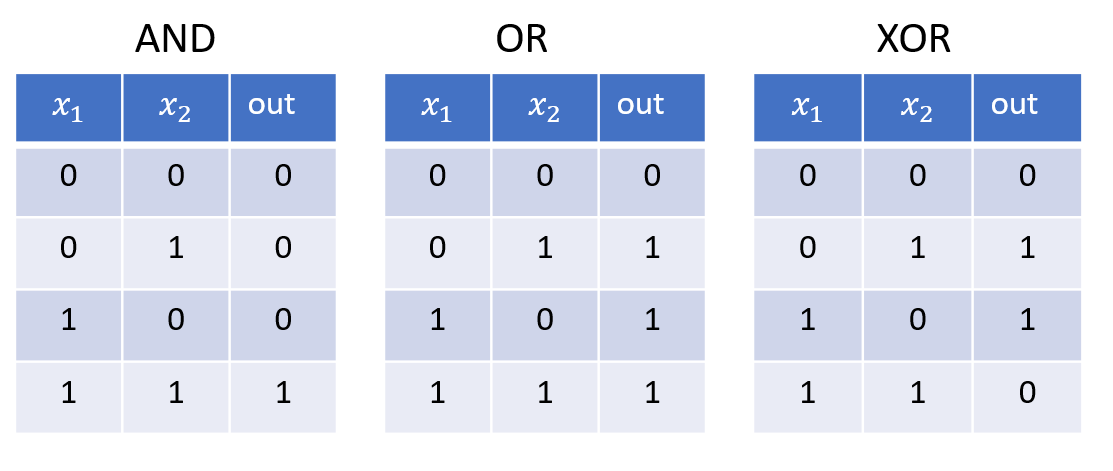
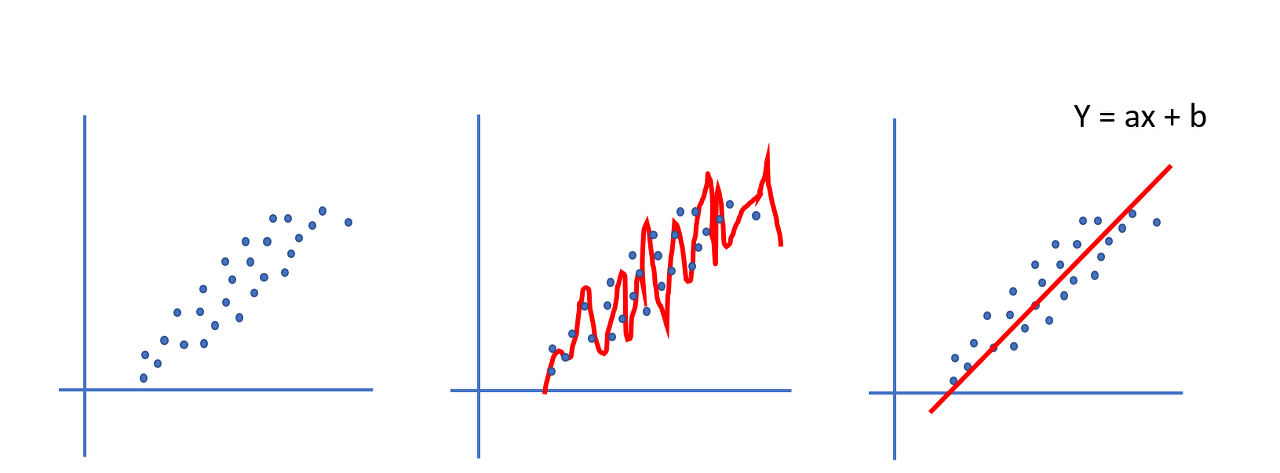
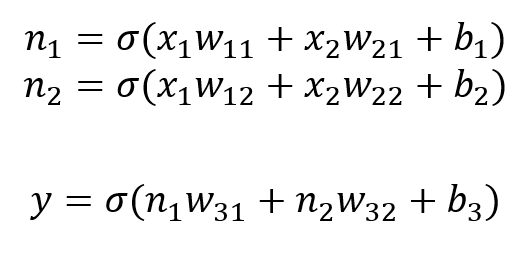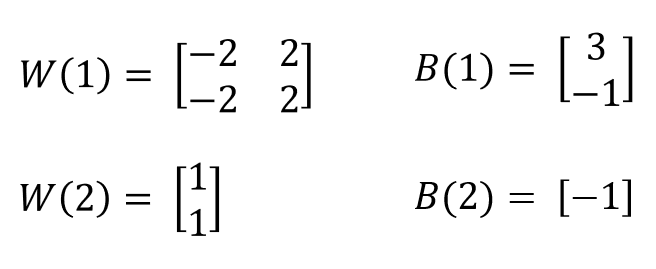파이썬 리스트는 활용도가 높지만, 빅데이터 처리에는 충분하지 않다. 

파이썬의 리스트에서는 데이터가 비연속적인 위치에 저당되므로 대량의 데이터 처라에 불리함. 

C언어 스타일의 2차원 배열은 데이터들이 연속적인 위치에 저장되어 효율적으로 처리할 수 있음. 왜냐하면 연속적으로 데이터가 저장되어 있어야 다음 데이터를 찾기 쉽기 때문. 

NumPy(Numerical Python):

과학/공학 분야에서 사용되는 파이썬 라이브러리

넘파이 API는 Pandas, SciPy, Matplotbli, scikit-learn 등의ㅐ 패키지에서 사용됨. 

훈련샘플은 2차원, 3차원 다차원 행렬안에 저장됨. 

행렬에서 삭제, 분리, 추가 등의 조작은 반드시 넘파이를 사용

넘파이 불러오기

>>> import numpy as np

배열 생성하기

배열은 넘파이의 핵심 데이터 구조

배열의 요소는 모두 동일한 타입

배열의 랭크(rank)는 차원 수

배열의 형상(shape)은 각 차원 및 항목 수

** 1차원 배열은 하나의 축만 가지고 있고, 2차원 배열은 2개의 축을 가진다.

배열생성은 array 함수 사용

a = np.array([1,2,3])  ## 1차원

#  a: 배열 객체

#  np.arry: 생성자 함수 

#  ([1,2,3]) : 파이썬 리스트

>>> a

array([1,2,3])

>>> a[0]

1

>>> b = np.array([[1,2,3],[4,5,6],[7,8,9]])

>>> b

arrary([[1,2,3],

         [4,5,6],

         [7,8,9]])

>>> b[0][2]

3

배열의 속성

넘파이 클래스 ndarray의 속성들

ndim : 축의 갯수, 2차원이면 ndim=2

shape: 배열의 형상, 정수 튜플로 나나냄. n행, m열의 경 (n,m)

size: 배열 내 요소들의 총 갯수

dtype: 배열 요소의 자료형,. numpy.int32, numpy.int16, numpy.float64 등

itemsize: 배열을 이루는 요소의 크기. 단위는 바이트. float64는 itemsize=8

data: 실제 데이터가 저장되는 메모리 블럭 주소

넘파이 배열 자료형 지정:

>>> dtype = np.int32  또는 dtype="np.int32"

>>> a=np.array([[0,1,2],

                      [3,4,5],

                      [6,7,8]])

>>> a.shape       # 배열의 형상

(3,3)

>>> a.ndim        # 배열의 차원 수

2

>>> a.dtype       # 요소의 자료형

dtype('int32')

>>> a.itemsize     # 요소 한개의 크기

8

>>> a.size   # 전체 요소 수 

9

1 또는 0으로 채워진 배열 생성 (주로 배열 초기화에 사용됨)

>>> np.zeros((3,4))
array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])
>>> np.ones((3,4))
array([[1., 1., 1., 1.],
       [1., 1., 1., 1.],
       [1., 1., 1., 1.]])
>>> np.ones((3,4), dtype=np.int32)
array([[1, 1, 1, 1],
       [1, 1, 1, 1],
       [1, 1, 1, 1]])
>>> np.eye(3)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

>>> x = np.ones(5, dtype=np.int64)
>>> x
array([1, 1, 1, 1, 1], dtype=int64)

연속되는 값으로 배열 생성하기 

np.arange(start, stop, step)

>>> x = np.ones(5, dtype=np.int64)
>>> x
array([1, 1, 1, 1, 1], dtype=int64)
>>> np.arrange(5)
AttributeError: module 'numpy' has no attribute 'arrange'
>>> np.arange(5)
array([0, 1, 2, 3, 4])
>>> np.arange(1,6)
array([1, 2, 3, 4, 5])
>>> np.arange(1,6)
array([1, 2, 3, 4, 5])
>>> np.arange(1,10,2)
array([1, 3, 5, 7, 9])

np.linspace(start, stop, num)

start: 시작값

stop: 종료값

num: 갯수

>>> np.linspace(0,10,100)
array([ 0.        ,  0.1010101 ,  0.2020202 ,  0.3030303 ,  0.4040404 ,
        0.50505051,  0.60606061,  0.70707071,  0.80808081,  0.90909091,
        1.01010101,  1.11111111,  1.21212121,  1.31313131,  1.41414141,
        1.51515152,  1.61616162,  1.71717172,  1.81818182,  1.91919192,
        2.02020202,  2.12121212,  2.22222222,  2.32323232,  2.42424242,
        2.52525253,  2.62626263,  2.72727273,  2.82828283,  2.92929293,
        3.03030303,  3.13131313,  3.23232323,  3.33333333,  3.43434343,
        3.53535354,  3.63636364,  3.73737374,  3.83838384,  3.93939394,
        4.04040404,  4.14141414,  4.24242424,  4.34343434,  4.44444444,
        4.54545455,  4.64646465,  4.74747475,  4.84848485,  4.94949495,
        5.05050505,  5.15151515,  5.25252525,  5.35353535,  5.45454545,
        5.55555556,  5.65656566,  5.75757576,  5.85858586,  5.95959596,
        6.06060606,  6.16161616,  6.26262626,  6.36363636,  6.46464646,
        6.56565657,  6.66666667,  6.76767677,  6.86868687,  6.96969697,
        7.07070707,  7.17171717,  7.27272727,  7.37373737,  7.47474747,
        7.57575758,  7.67676768,  7.77777778,  7.87878788,  7.97979798,
        8.08080808,  8.18181818,  8.28282828,  8.38383838,  8.48484848,
        8.58585859,  8.68686869,  8.78787879,  8.88888889,  8.98989899,
        9.09090909,  9.19191919,  9.29292929,  9.39393939,  9.49494949,
        9.5959596 ,  9.6969697 ,  9.7979798 ,  9.8989899 , 10.        ])

배열 정렬

>>> arr = np.array([2,1,5,3,7,4,6,8])
>>> np.sort(arr)

배열 합치기

array([1, 2, 3, 4, 5, 6, 7, 8])
>>> x=np.array([[1,2],[3,4]])
>>> y=np.array([[5,6],[7,8]])
>>> np.concatenate((x,y), axis=1)
array([[1, 2, 5, 6],
       [3, 4, 7, 8]])

2개 배열 수직으로 쌓기

np.concatenate(), vstack(), hstack() 사용해도 됨.

>>> np.vstack((x,y))
array([[1, 2],
       [3, 4],
       [5, 6],
       [7, 8]])
>>> np.vstack(x,y)
TypeError: _vhstack_dispatcher() takes 1 positional argument but 2 were given
>>> np.hstack((x,y))
array([[1, 2, 5, 6],
       [3, 4, 7, 8]])

배열 형태 변환

일반적으로 딥러닝은 2차원 입력이어야 한다.

따라서, 1차원 자료를 2차원으로 변환해야 

reshape(): 행렬 데이터 갯수는 그대로, 차원만 변경함. 

new_array = old_array.reshape((2,3))

new_array: 새로운 배열

old_array: 원래 배열

(2,3): 새 배열 형상

>>> a = np.arange(12)
>>> a.shape
(12,)
>>> a.reshape(3,4)   # 3x4 행렬로 변환
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> a.reshape(6,-1)    #인수가 -1 인 경우, 데이터 갯수에 맞춰서 자동으로 배열형태 결정함. 
array([[ 0,  1],
       [ 2,  3],
       [ 4,  5],
       [ 6,  7],
       [ 8,  9],
       [10, 11]])

다차원 배열 평탄화

다차원 배열 --> 1차원으로 

flatten() 사용 (ravel() 사용하면 view 만 변경되므로 주의.)

>>> y = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
>>> y.flatten()
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

>>> a = y.flatten()
>>> a[0]= 99
>>> print(a)
[99  2  3  4  5  6  7  8  9 10 11 12]
>>> print(y)
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]

배열 분할(슬라이싱)

넘파이 배열을 자르는 메소드는 split()

세로로 자르려면 axis=1,가로면 axis=0

>>> array= np.arange(30).reshape(-1,10)
>>> array
array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24, 25, 26, 27, 28, 29]])
>>> array= np.arange(30).reshape(-1,10)
>>> array
array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24, 25, 26, 27, 28, 29]])
>>> arr1,arr2 = np.split(array, [3], axis=1)
>>> arr1
array([[ 0,  1,  2],
       [10, 11, 12],
       [20, 21, 22]])
>>> arr2
array([[ 3,  4,  5,  6,  7,  8,  9],
       [13, 14, 15, 16, 17, 18, 19],
       [23, 24, 25, 26, 27, 28, 29]])

배열에 새로운 축 추가하기

np.newaxis, np.expand_dims를 사용하여 기존 배열의 크기를 증가시킬 수 있음

np.newaxis를 사용할 때 마다 차원이 1차원 증가

>>> a = np.array([1,2,3,4,5,6])
>>> a.shape
(6,)
>>> a1=a[np.newaxis, :]
>>> a1.shape
(1, 6)
>>> a2=a[:, np.newaxis]

array([[1],
       [2],
       [3],
       [4],
       [5],
       [6]])
>>> a2.shape
(6, 1)

np.expand_dims() 를 사용하여 지정된 위치에 새 축을 삽입하여 배열 확장 가능

>>> b = np.expand_dims(a, axis=1)
>>> b
array([[1],
       [2],
       [3],
       [4],
       [5],
       [6]])
>>> b.shape
(6, 1)

인덱싱과 슬라이싱

>>> ages = np.array([18,19, 25, 30, 28])
>>> ages[1:3]    # index 1~2
array([19, 25])
>>> ages[:2]      # index 0~1
array([18, 19])
>>> y = ages > 20     # 논리 인덱싱
>>> y 
array([False, False,  True,  True,  True])

>>> ages[ages > 20]  ## 20 이상을 뽑아낼 때

array([25,30,28])

2차원 배열의 인덱싱

2차원 배열 인덱싱/슬라이싱은 가장 많이 사용됨. 연습 필요. 

>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> a[0,2]
3
>>> a[0][2]
3
>>> 

>>> a[0,0] = 12
>>> a
array([[12,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9]])

2차원 배열 슬라이싱

>>> a[0:2, 1:3]
array([[2, 3],
       [5, 6]])

>>> a[0]

array([1,2,3])

>> a[1,1:3]

array([5,6])

얕은 복사와 깊은 복사

넘파이 함수, 인덱싱, 슬라이싱 연산자는 데이터 복사 필요없이 view 만 변환

view에서 데이터 수정하면 원본 배열도 수정됨. 

얕은 복사 예 ... b가 변하면 원본 a도 변한다.

>>> a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
>>> b = a[0,:]
>>> b
array([1, 2, 3, 4])
>>> b[0] = 99

>>> b
array([99, 2, 3, 4])
>>> a
array([[99,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

깊은 복사 예  ... b2는 변해도 원본 a는 변하지 않는다.

>>> b2 = a.copy()
>>> b2
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
>>> b2[0] = 88
>>> b2
array([[88, 88, 88, 88],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
>>> a
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

기본 배열 연산

>>> arr1 = np.array([[1,2],[3,4],[5,6]])
>>> arr2 = np.array([[1,1],[1,1],[1,1]])
>>> results = arr1 + arr2
>>> results
array([[2, 3],
       [4, 5],
       [6, 7]])
>>> arr1**2
array([[ 1,  4],
       [ 9, 16],
       [25, 36]], dtype=int32)

>>> arr1.sum()

21

>>> arr1.min()

1

>>> arr1.max()

6

>>> arr1.mean(axis=0)   # 특정 열에서의 모든 행의 값을 사용해서 계산

array([3., 4.,])

>>> arr1.mean(axis=1)   # 특정 열에서의 모든 열의 값을 사용해서 계산

array([1.5, 3.5, 5.5]

>>> print(arr1.T)   # 전치행렬

>>> arr1*arr2
array([[1, 2],
       [3, 4],
       [5, 6]])

>>> arr1 = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> arr2 = np.array([[2,2],[2,2],[2,2]])
>>> arr1 @ arr2     ## 내적 (1번째 열, 2번째 행 갯수 일치해야)
array([[12, 12],
       [30, 30],
       [48, 48]])

난수 생성

>>> np.random.seed(100) # 이후 아래 명령어 수행해야

>>>np.radom.rand(5)

>>> np.radom.rand(5,3)

>>> np.radom.randit(1,7,size=10)

>> > np.random.randn(5)  ## 정규분포 난수 생성

 a  = np.random.normal(loc=0.0, scale=1.0, size=None)

loc: 평균

scale: 표준편차

size: 배열의 차원

>> mu, sigma = 0, 0.1

>> np.random.normal(mu, sigma, 5)

array([-0.17497655,  0.03426804,  0.11530358, -0.0252436 ,  0.09813208])

고유 항목과 갯수 구하기 

>>> a = np.array([11,11,12,14,13, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
>>> unique_values = np.unique(a)
>>> unique_values
array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20])
>>> uniuqe_values, indices_list = np.unique(a, return_index=True)

>>> print(indices_list)

[ 0 2 3 4 5 6 7 8 12 13 14]
>>> unique_values, occurrence_count = np.unique(a, return_counts=True)
>>> print(occurrence_count)
[3 2 2 2 1 1 1 1 1 1]

파일 입출력 (.csv)

Pandas 를 사용

read_csv()를 호출하면 반환되는 객체의 values에 넘파이배열로 저장됨. 

>>> import numpy as np

>>> import pandas as pd

>>> x= pd.read_csv('example.csv',  header=0).values  

>>> print(x)

>>> x= pd.read_csv('example.csv',  usecols=['col1','col2']).values  

>>> print(x)

>>> df = pd.DataFrame(a)

>>> print(df)

>> df.to_csv('out.csv')

epochs=5

batch_size=5
np.random.seed(1)

epochs=5

batch_size=5
np.random.seed(7820)

gap-filling with mean values.

epochs=20
batch_size=5
np.random.seed(7820)

from keras.models import Sequential
from keras.layers import Dense
classifier = Sequential()
classifier.add(Dense(units = 13, activation = 'relu'))
classifier.add(Dense(units = 1, activation = 'sigmoid'))
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

분류와 회귀에서 사용하는 용어 정리

샘플(입력): 학습 모델에 들어갈 하나의 데이터 

예측(출력): 모델 결과 값

타깃(정답): 모델이 완벽하게 예측해야 하는 값

참값(꼬리표, annotation): 일반적으로 사람에 의해 수집된 데이터셋에 대한 모든 타깃.

예측오차(손실값): 모델의 예측과 타깃 사이의 (거리) 차이값

클래스: 분류 문제에서 선택할 수 있는 레이블의 집합.

          예) 고양이-강아지 분류 문제에서 클래스는 "고양이"와 "강아지" 2개

레이블: 분류

1. 지도 학습

가장 흔한 학습 방법

주어진 샘플 데이터의 (사람이 만든)레이블 또는 꼬리표(annotation)에 입력 데이터를 매핑하는 방법을 학습시킴

대부분 분류와 회귀 문제로 구성됨

예) 구문 트리 예측, 물체 감지

2. 비지도 학습

타깃없이 입력 데이터의 변환을 찾는 학습방법

데이터 시각화, 데이터 압축, 데이터 노이즈 제거, 데이터 상관관계를 더 잘 이해하기 위해 사용

지도학습 문제를 풀기 전에 데이터셋을 잘 이해하기 위해 사용하는 필수 단계로 이용되기도 함

예) 차원축소, 군집

3. 자기 지도 학습(self-supervised learning)

사람이 만든 레이블을 사용하지 않음으로 학습 과정에 사람이 개입하지 않는 지도 학습.

예) 오토인코더(autoencoder), 비디오 다음 프레임 예측, 다음 단어 예측

4. 강화학습

구글 딥마인드의 아타리 게임과 알파고 바둑대국 성공으로 주목 받기 시작함.

환경에 대한 정보를 받아 보상을 최대화하는 행동을 선택하도록 학습시킴

예를 들어, 게임 점수를 최대화하기 위한 게임 내의 행동을 출력

대부분 연구영역, 게임 외 성공 사례가 없음.

예) 자율 주행 자동차, 자원 관리, 교육

MNIST 데이터베이스 (Modified National Institue of Standards and Technology database)

손글씨 이미지 데이터셋 

0에서 9까지 10가지로 분류될 수 있는 손글씨 숫자 이미지 70,000개

각 이미지는 28×28 픽셀로 구성

각 픽셀은 아래와 같이 0~255 사이의 숫자 행렬로 표현됩니다.

[[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   3  18  18  18 126 136 175  26 166 255 247 127   0   0   0   0]
[  0   0   0   0   0   0   0   0  30  36  94 154 170 253 253 253 253 253 225 172 253 242 195  64   0   0   0   0]
[  0   0   0   0   0   0   0  49 238 253 253 253 253 253 253 253 253 251  93  82  82  56  39   0   0   0   0   0]
[  0   0   0   0   0   0   0  18 219 253 253 253 253 253 198 182 247 241   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0  80 156 107 253 253 205  11   0  43 154   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0  14   1 154 253  90   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0 139 253 190   2   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0  11 190 253  70   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0  35 241 225 160 108   1   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0  81 240 253 253 119  25   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0  45 186 253 253 150  27   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0  16  93 252 253 187   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 249 253 249  64   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0  46 130 183 253 253 207   2   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0  39 148 229 253 253 253 250 182   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0  24 114 221 253 253 253 253 201  78   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0  23  66 213 253 253 253 253 198  81   2   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0  18 171 219 253 253 253 253 195  80   9   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0  55 172 226 253 253 253 253 244 133  11   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0 136 253 253 253 212 135 132  16   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]]

 60,000개의 이미지는 훈련 (Training)에 사용

10,000개의 이미지는 테스트 (Test)에 사용

코드

1. tensorflow 불러오기

# Tf를 쓰면 무려 Mnist 데이터를 다운받지 않아도 됨.

>>> import tensorflow as tf             

2. MNIST 데이터셋 불러오기 (import)

# Tf에서는 train / test set을 자동으로 나눔.

>>> mnist = tf.keras.datasets.mnist
>>> (x_train, y_train), (x_test, y_test) = mnist.load_data()    

3. 데이터 전처리 
# mnist 데이터는 0~255 범위의 데이터

# 딥러닝은 0~1 사이로 input 데이터의 범위를 해줘야 원활한 학습이 가능.
# 0~1 사이로 맞춰주기 위해서 255로 나눔.
>>> x_train, x_test = x_train / 255.0, x_test / 255.0
>>> x_train.shape

4. 모델구성

# tf.keras.models.Sequential()을 이용해서 인공신경망 모델을 구성

>>> model = tf.keras.models.Sequential([
# 입력층 (Input layer)에서 Flatten()을 이용해서 28×28 픽셀의 값을 784개의 1차원 배열로 변환

...   tf.keras.layers.Reshape((28, 28, 1)),  

# 각 층은 512개와 10개의 인공 뉴런 노드를 갖고 활성화 함수 (activation function)로는 각각 ReLU (tf.nn.relu)와 소프트맥스 (tf.nn.softmax) 사용.
...   tf.keras.layers.Conv2D(16, 3, activation='relu'),
...   tf.keras.layers.Flatten(),
...   tf.keras.layers.Dense(128),
...   tf.keras.layers.Dense(10, activation='softmax')
... ])

5. 모델 컴파일

>>> model.compile(optimizer='adam',
...   loss='sparse_categorical_crossentropy',
...   metrics=['accuracy'])

6. 모델 훈련

>>> model.fit(x_train, y_train, epochs=5)

7. 모델 평가

# model.evaluate()를 이용해서 10,000개의 테스트 샘플에 대해 손실 (loss)과 정확도 (accuracy)를 평가

>>>  test_loss, test_acc = model.evaluate(x_test, y_test)

>>> print('테스트 정확도:', test_acc)

# Matplotlib을 이용해서 에포크에 따른 정확도 (accuracy)와 손실 (loss) 값을 확인

>>>loss, accuracy = [], []

>>>for i in range(10):

...   model.fit(x_train, y_train, epochs=1)

...   loss.append(model.evaluate(x_test, y_test)[0])

...   accuracy.append(model.evaluate(x_test, y_test)[1])

>>>print(accuracy)

코드 (copy & paste & run)

import tensorflow as tf
# Tf를 쓰면 무려 Mnist 데이터를 다운받지 않아도 됩니다.
mnist = tf.keras.datasets.mnist
# 또한 train / test set을 알아서 나눠 줍니다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# mnist 데이터는 0~255 범위의 데이터 입니다. 
# 이를 0~1 사이로 맞춰주기 위해서 255로 나누는 것인데 
# 딥러닝은 0~1 사이로 input 데이터의 범위를 해줘야 학습이 잘 됩니다.
x_train, x_test = x_train / 255.0, x_test / 255.0

x_train.shape

model = tf.keras.models.Sequential([
  tf.keras.layers.Reshape((28, 28, 1)),
  tf.keras.layers.Conv2D(16, 3, activation='relu'),
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(128),
  tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

model.fit(x_train, y_train, epochs=5)

## 모델 평가
# model.evaluate(x_test,  y_test, verbose=2)
# 코드를 읽고, 코딩하기도 편하게 따로 불러와줍니다.


test_loss, test_acc = model.evaluate(x_test, y_test)
print('테스트 정확도:', test_acc)

#1회의 에포크마다 model.evaluate()의 loss, accuracy 값을 출력력
loss, accuracy = [], []
for i in range(10):
    model.fit(x_train, y_train, epochs=1)
    loss.append(model.evaluate(x_test, y_test)[0])
    accuracy.append(model.evaluate(x_test, y_test)[1])

print(accuracy)
# end of code

기울기 소실 문제(vanishing gradient)

• 출력층에서 은닉층을 역방향으로 하나씩 진행하며, 각 층(은닉층, 입력층)의 가중치를 수정하는 방법
• 가중치 수정을 위해서는 미분값(기울기)가 필요

• 

• 층의 갯수가 늘어나면, 역전파를 통해 전달되는 기울기 값이 점점 작아져, 맨 처음층(입력층)까지 도달하지 않는 문제가 발생... 기울기 소실 문제(vanishinig gradient)
• 활성화 함수(시그모이드 함수)의 특징 때문에, 여러 층을 거칠 수록 기울기가 사라져서 가중치 수정이 어려워짐.

활성화 함수

1. Sigmoid 함수

• 미분하면 최대치가 < 1.0 따라서, 계속 곱하면 0에 수렴.... 기울기 소실 발생

2. tanh 함수

• 시그모이드 함수 확장형 [-1,1]
• 1보다 작은 값이 존재하므로, 기울기 소실 발생

기울기 소실 문제를 해결하기 위해서 새로운 활성화 함수가 필요. 

3. ReLU 함수

• 0보다 작을때 0으로 처리, 0보다 클때 x값을 그대로 사용 ... 기울기 소실 해결

4. Softplus 함수

• ReLU함수에서 0보다 작은 경우를 완화한 함수... 기울기 소실 해결

그 외 다양한 활성화 함수

Activation Functions : Sigmoid, tanh, ReLU, Leaky ReLU, PReLU, ELU, Threshold ReLU and Softmax basics for Neural Networks and Deep Learning | by Himanshu S | Medium