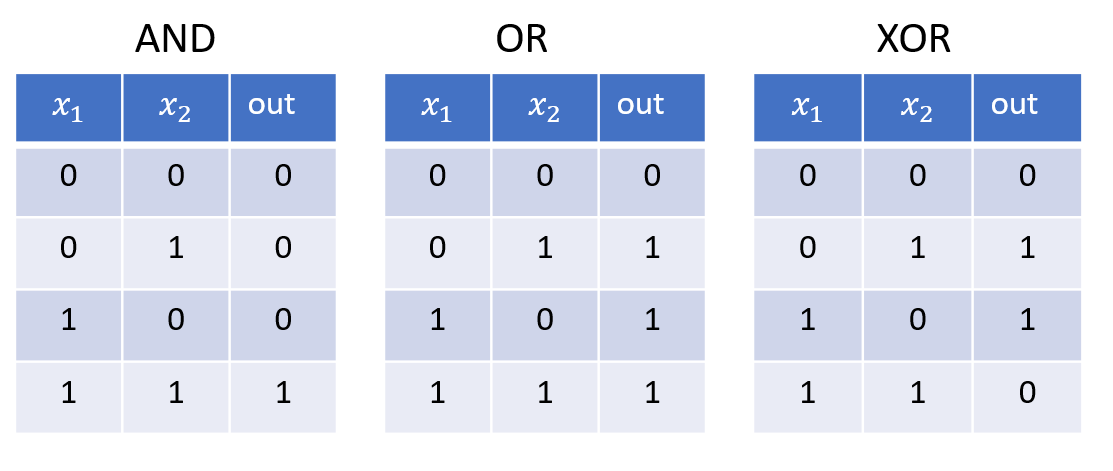
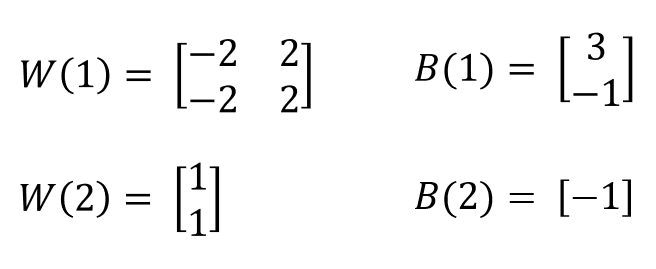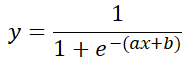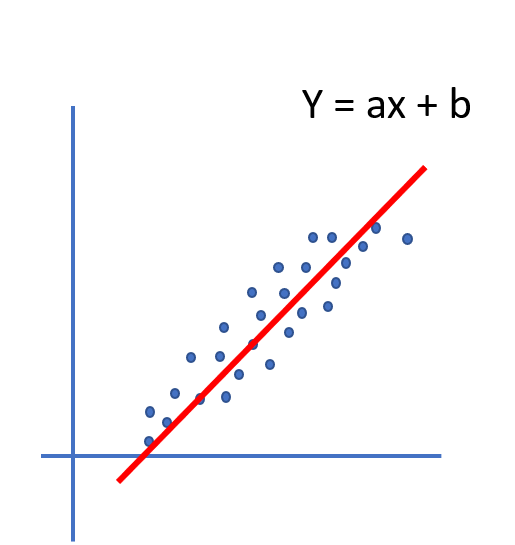진리표
컴퓨터 디지털 회로 gate 논리
AND: 둘다 1 이면 1
OR: 둘 중 하나라도 1 이면 1
XOR: 둘 중 하나만 1이면 1
분류기 퍼셉트론

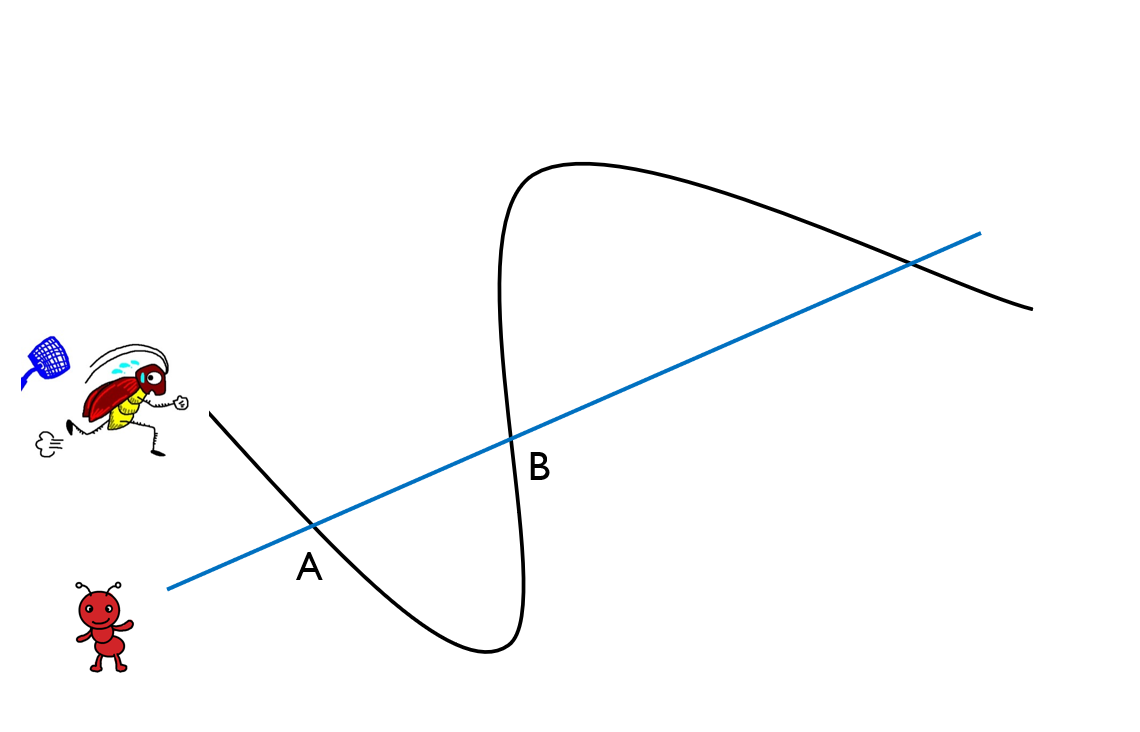
XOR (exclusive OR) 문제
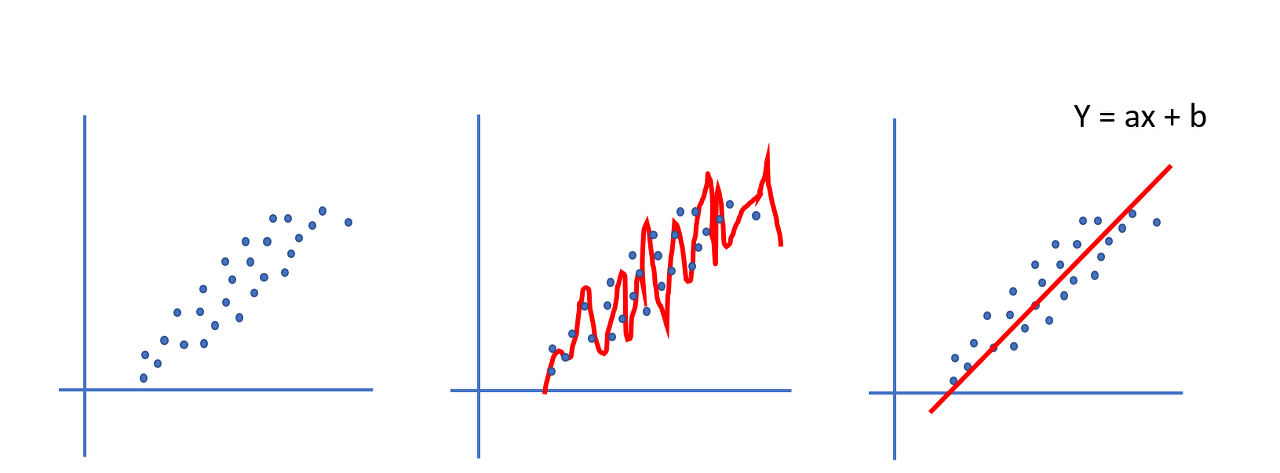
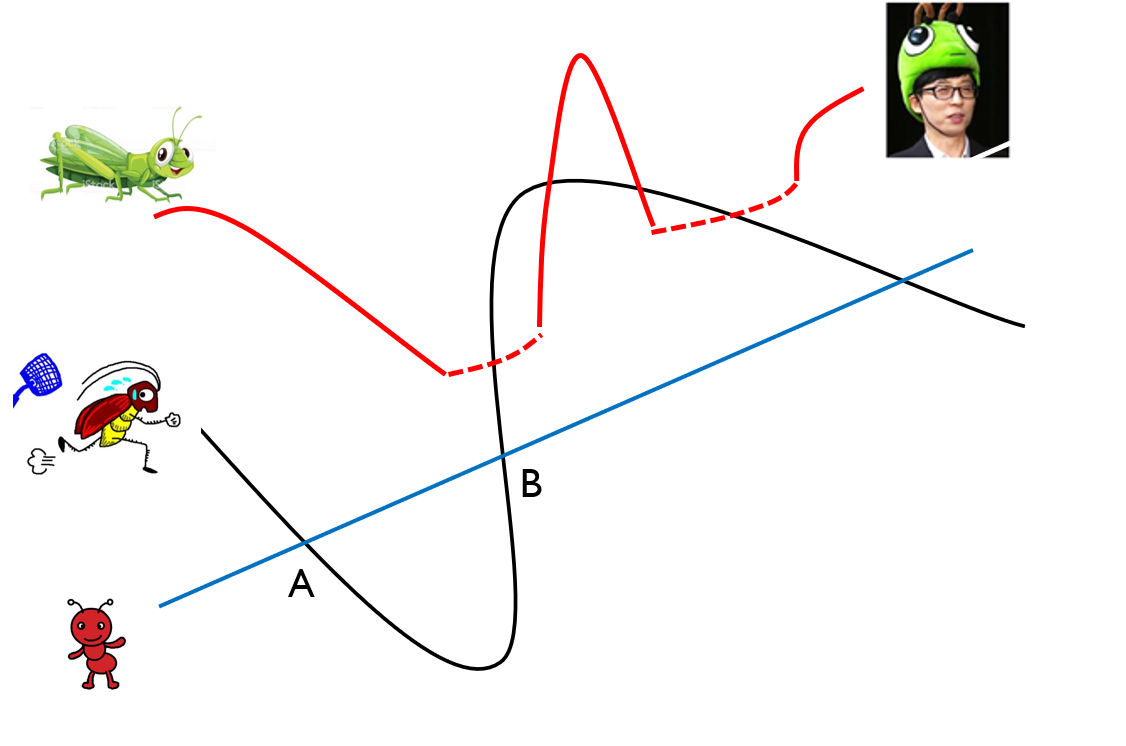
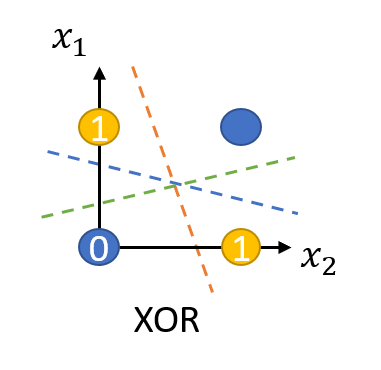
- 그림처럼, 각각 두 개씩 다른 점이 있다고 할 때, 하나의 선을 그어 색깔별로 분류하는 방법을 생각해 보자.
- 어떠한 한 개의 직선으로도 분류할 수 없다.... 1969년 Marvin Minsky 가 발견
XOR 문제 해결
- 1990년대 다층 퍼셉트론(multilayer perceptron)으로 해결
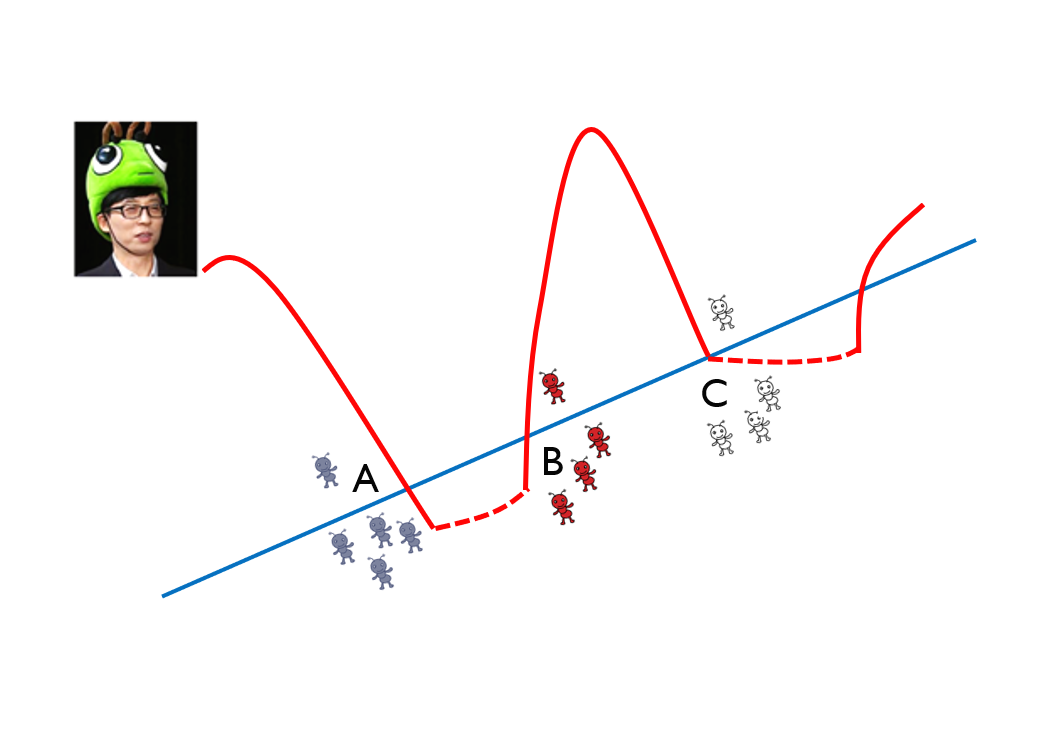
- 아래 그림과 같이 2차원 평면 공간을 3차원으로 확장해서 분류할 수 있음.
- 즉, 차원 확장과 좌표 평면 변환 이용

- XOR 문제를 해결하기 위해서는 2개의 퍼셉트론을 한번에 계산할 수 있어야 함.
- 은닉층(hidden layer)을 가진 다층 퍼셉트론을 구현하여 가능.
다층 퍼셉트론

1. 각 퍼셉트론의 가중치(w)와 바이어스(b)를 은닉층의 노드(n)로 보냄.
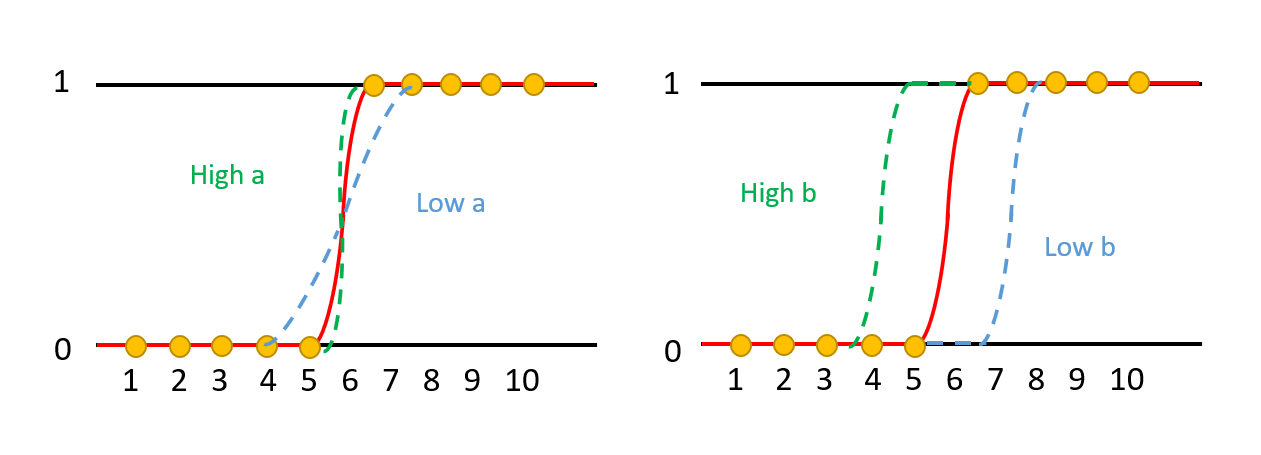
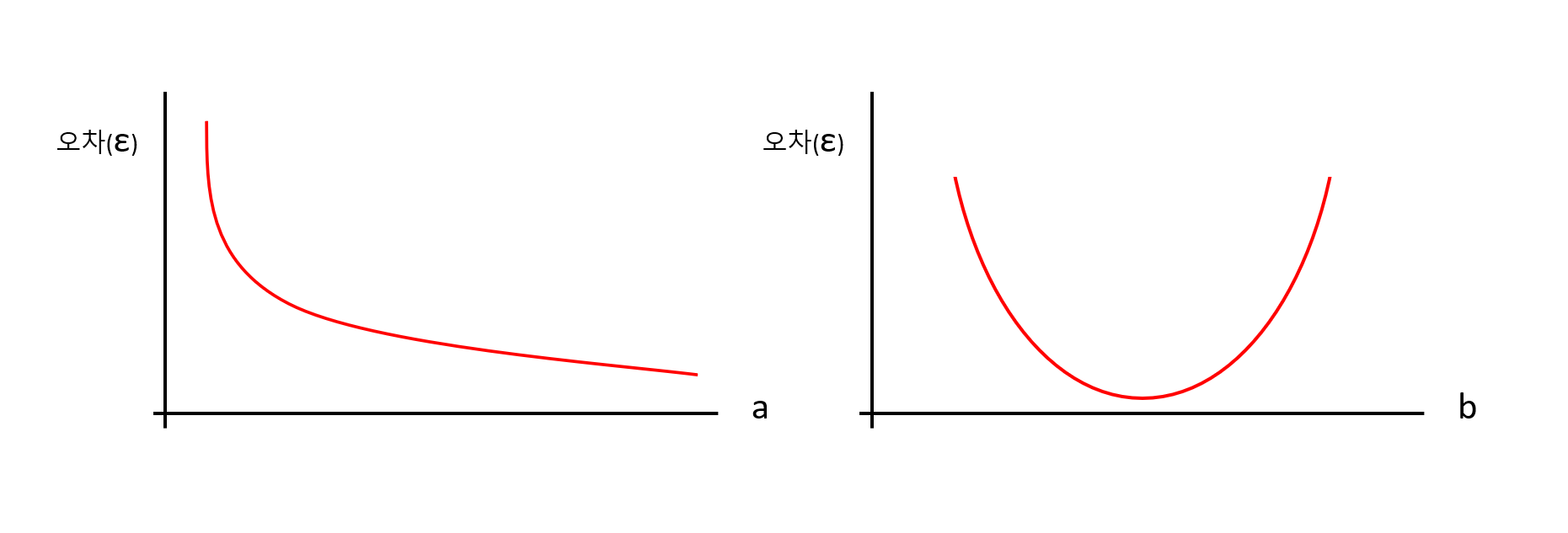
2. 은닉층으로 들어온 w, b에 시그모이드 함수를 적용하여 최종 결과값을 출력함

w와 b를 구하기 위해서 행렬로 표현하면,
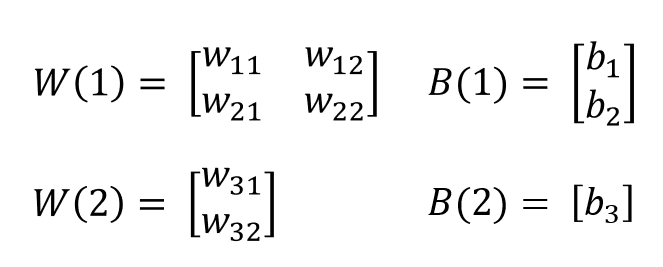
연습: XOR 문제 해결
아래 예제를 통해서, XOR 진리표를 구할 수 있는지 연습해 보자.
먼저 각 노드 n1, n2를 구하고, 최종 y 출력값을 계산한다.