에러:
ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
해결:
model = LogisticRegression(random_state=42) 을
model = LogisticRegression(random_state=42, solver='lbfgs', max_iter=100) 로 수정한다.
에러:
ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
해결:
model = LogisticRegression(random_state=42) 을
model = LogisticRegression(random_state=42, solver='lbfgs', max_iter=100) 로 수정한다.
(base) conda info --envs
(base) conda list
(base) conda remove --prefix [PATH] --all
(base) conda remove --name --all
(base) activate test
(test)
명령어 conda 나 pip 가 같은 역할의 명령을 수행함.
주의: 모듈을 설치할때는 conda 대신 pip 사용하길 추천함 (아래 글 참고). 버전 충돌이나 miniconda 충돌 등이 발생할 수 있음.
Tensorflow GPU 작동하지 않을때, 재설치 없이 수리하는 법
본 문서는 NVIDIA 그래픽 카드와 Anaconda를 설치했음에도 tensorflow_gpu가 작동하지 않은 경우, 모든 설치 앱을 갈아없지 않고 수리하는 방법을 정리한 것임. 증상 아래 그림에서 CPU만 인식한다. 몇 번
aeir.tistory.com
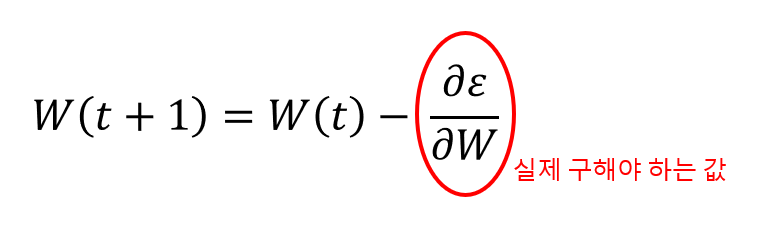

1. Sigmoid 함수
기울기 소실 문제를 해결하기 위해서 새로운 활성화 함수가 필요.
Activation Functions : Sigmoid, ReLU, Leaky ReLU and Softmax basics for Neural Networks and Deep…
Let’s start with the basics why would we even need an activation function and what is it >
himanshuxd.medium.com
여기서는 모델이 수행되는 과정에서는 에러가 없었으나, 최종 결과가 loss: NaN, accuracy:NaN, mae:NaN 등으로 나오는 경우, 필자가 찾아낸 문제해결 법이다.
지금까지 2가지 경우에 대해서 경험하였고, 다음과 같이 해결할 수 있다.
이때 아래와 같이 데이터 셋에서 NA를 제거해 준 다음 사용하면 된다.
> data.set <- na.omit(<INPUT DATA>)
> str(data.set)
1번으로 해결되지 않을 때, layer_dense 내 activation 함수를 "softmax"에서 "relu"로 바꾸면 된다. single output 인 경우, softmax를 사용하면 이런 현상이 발생할 수 있다. 여기(https://github.com/keras-team/keras/issues/2134) 내용의 댓글들을 참고하시오.
아래 블로그를 참조하시라.
책이나 사이트에 공개된 잘 만들어진 예제를 이용해서, 자신의 데이터에 바로 적용할 때, 필자와 같은 왕초보들은 항상, as always, as usual, 필연적으로, 반드시, 운명적으로, .... 한방에 작동하지 않고 여러가지 문제들로 인해 머리가 지끈지끈 아픈 상황과 문제가 발생할 수 있다. 아니, 발생한다. 하나하나 잡아보자.
딥러닝 책 등에서 제공된 예제 파일들은 모두 Keras 등의 패키지 내에 포함된 예제 파일들이다. 그래서 실제 내가 만든 .csv 파일을 읽어 들이는데, 입력 포맷이 맞지 않아 헤맬 수 있다. 이런 경우, 모델이 잘 돌아가지만, input_data 값이 없다는 에러가 발생할 수 있다.
아래와 같이 sampling 하면, 일반 책에서 사용하는 예제 파일을 읽어들이는 포맷으로 쉽게 변환된다. 아래는 13개 컬럼으로 구성된 데이터 셋의 경우의 예임.
> set.seed(1)
# sample 함수는 수행할 때 마다 다른 난수를 추출하기 때문에 난수를 고정시켜 같은 값이 나오도록 하기 위함이다.
> smp = sample(1:nrow(<INPUT DATA>), nrow(<INPUT DATA>)/2)
# 2로 나눈 것은 절반의 데이터만 추출해서 쓰겠다는 의미
> train_data <- <INPUT DATA>[smp, 1:12]
> train_targets <- <INPUT DATA>[smp, 13]
> test_data <- <INPUT DATA>[-smp, 1:12]
> test_targets <- <INPUT DATA>[-smp, 13]
이 후 keras model을 구성하면 된다.
신경망은 순전파 해서 결과를 예측한다.
결과 레이어에 도달하기까지 모든 레이어에서의 연산이 포함된다.
1. 임의의 초기 가중치를 사용하여 처음 결과값(y)을 구함.
2. 그 결과값과 참값(예상 또는 기대하는 값) 사이의 평균 제곱 오차(ε)를 구함.
3. 이 오차를 최소로 만드는 지점으로 조금씩 거슬로 이동하면서 미분... 경사 하강법
4. 미분의 기울기가 0인(0으로 수렴되는) 지점이 최적화된(수정된) 최종 가중치.
최적화의 방향은 출력층에서 시작해서 입력층... 따라서 "오차 역전파"라고 부름
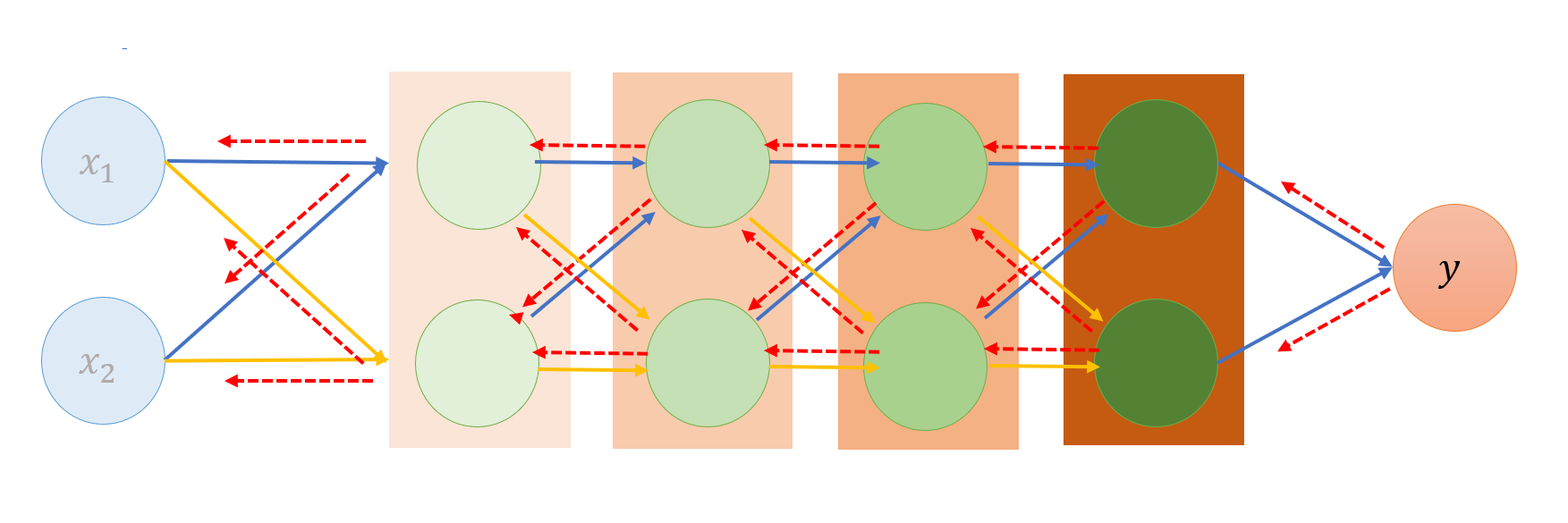
단일 퍼셉트론과 같은 원리이나, 은닉층의 가중치를 구해야 함.
1. 임의의 초기 가중치를 사용하여 처음 결과값(y)을 구함.
2. 그 결과값과 참값(예상 또는 기대하는 값) 사이의 평균 제곱 오차를 구함.
3. 경사 하강법을 이용하여, 오차가 작아지는(미분값이 0으로 수렴하는) 방향으로 이동시켜 가중치를 갱신함.
4. 오차가 더 이상 줄어들지 않을 때까지 (미분의 기울기가 0으로 수렴 할 때까지) 반복.
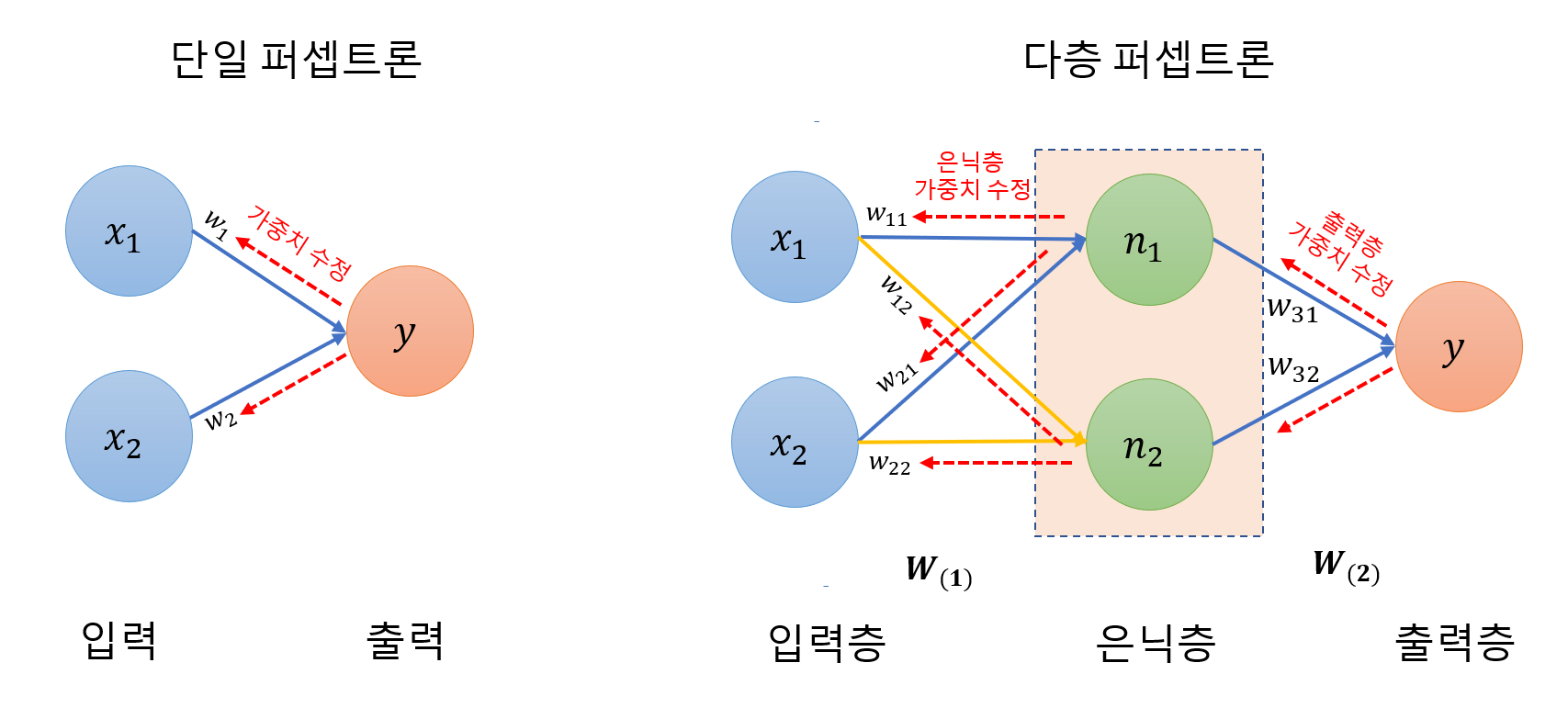

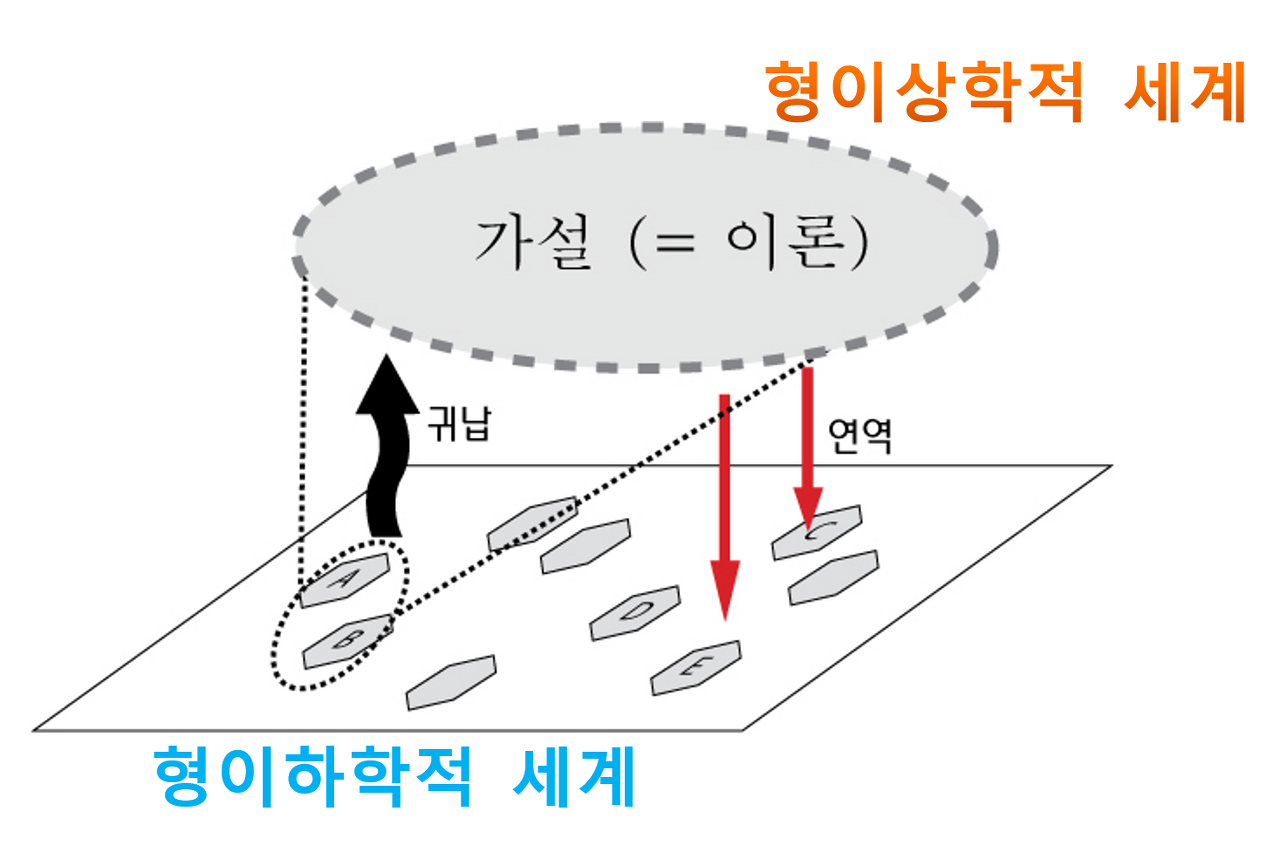
아래 그림과 같이 2차원 평면 공간을 3차원으로 확장해서 분류할 수 있음.
즉, 좌표 평면 변화를 적용.
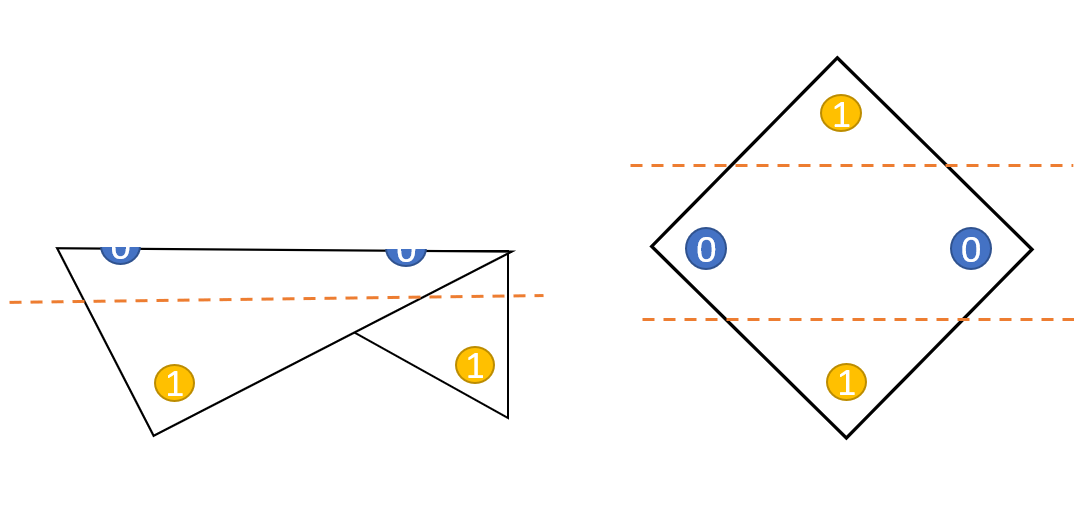
XOR 문제를 해결하기 위해서는 2개의 퍼셉트론을 한번에 계산할 수 있어야 하는데, 은닉층(hidden layer)를 사용하면 가능함.
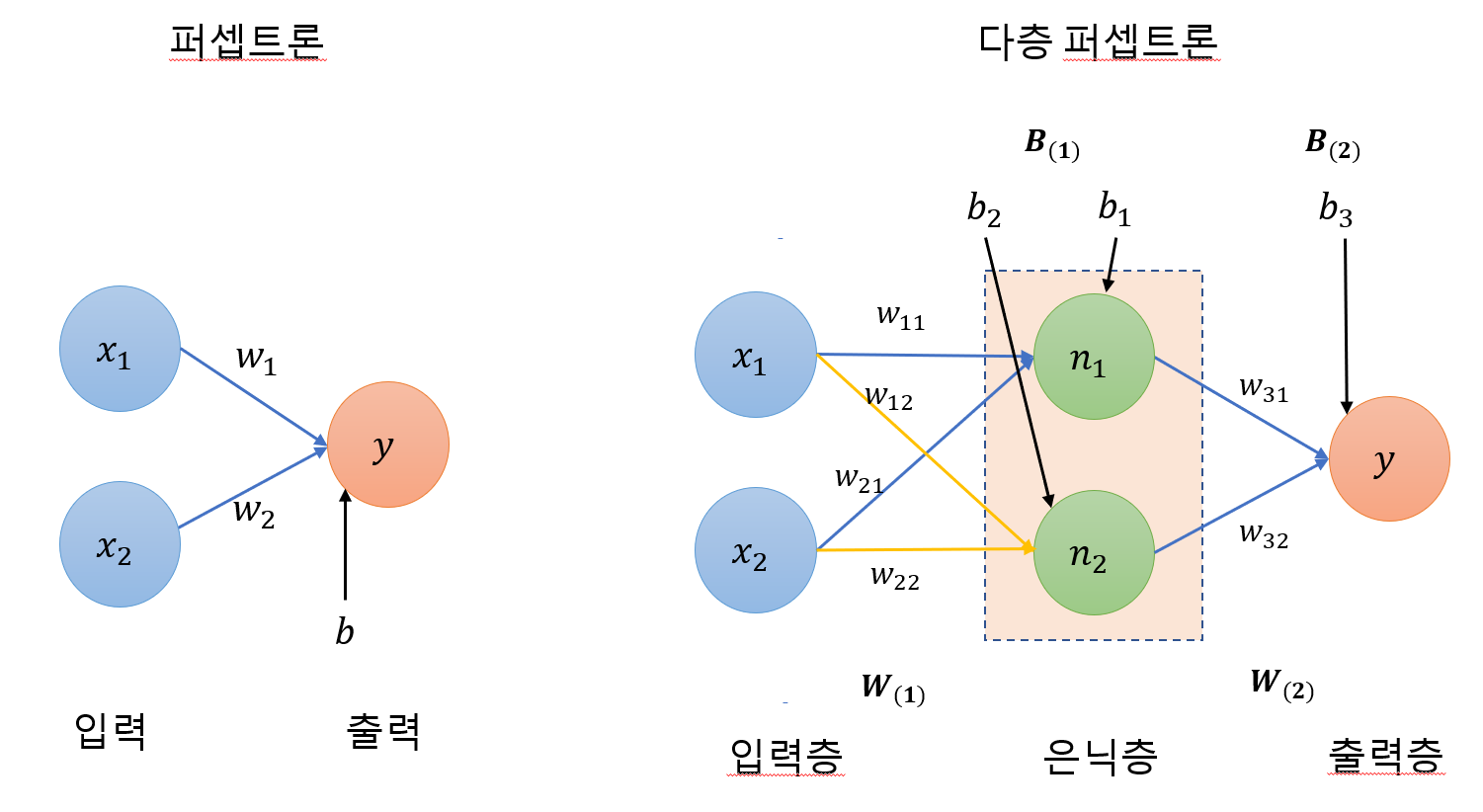
1. 각 퍼셉트론의 가중치(w)와 바이어스(b)를 은닉층의 노드(n)로 보냄.
2. 은닉층으로 들어온 w, b에 시그모이드 함수를 적용하여 최종 결과값을 출력함
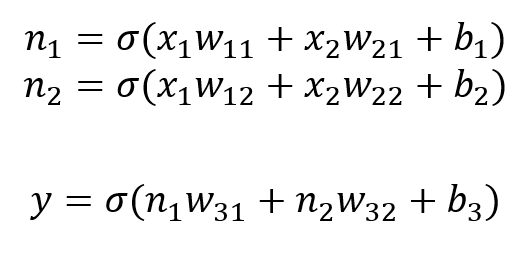
w와 b를 구하기 위해서 행렬로 표현하면,

아래 예제를 통해서, XOR 진리표를 구할 수 있는지 연습해 보자.
먼저 각 노드 n1, n2를 구하고, 최종 y 출력값을 계산한다.
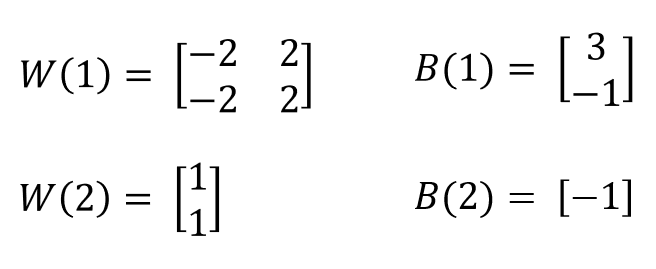



가중치(weight): 기울기 a1, a2를 퍼셉트론에서는 가중치(weight)라고 하고 w1, w2으로 표기
바이어스(bias): 절편 b는 퍼셉트론에서 편향(bias)라고 함.
가중합(weighted sum): 입력값(x)와 가중치(w)를 곱한 후 모두 더한 다음 바이어스(b)를 더한 값
활성화 함수: 0,1을 판단하는 함수. 예) 시그모이스 함수
- 2차원 이상의 함수에서 최저점(기울기, 절편)을 찾는 방법
- 오차의 변화의 2차 함수 그래프를 만들고 적절한 학습률을 설정해 기울기가 0인 지점을 구하는 것.
1. X1에서 미분으로 기울기 구함
2. 구해진 기우기의 반대방향으로 얼마간 이동시킨 X2에서 미분
(기울기가 +이면 음의 방향, 기울기가 -이면 양의 방향으로 이동시킴)
3. 미분 값이 0이 될때 까지 위 과정을 반복해서 최소값을 구함.

- 학습율을 너무 크게 설정하면, 기울기의 부호를 바꿔 이동할 때 적절한 거리는 찾지 못해 너무 멀리 이동하면, 기울기(a)가 수렴하지 않고 발산할 수 있음. -> overshooting
학습율을 너무 작게 하면 국소 최적치(local minima)에 빠져 최적화된 w를 찾기 전에 학습이 끝날 수 있다.
- 따라서, 이동거리를 정하는 것이 중요 ... 학습률 개념
- 딥러닝에서 학습률의 값을 적절히 바꾸면서 최적의 학습률을 찾는 것이, 최적화 과정 중의 하나. 일반적으로 0.01 을 초기값으로 하고 학습비용 (cost)를 관찰한 후 조금식 조정함.
- 경사 하강법은 오차 변화의 2차 함수 그래프를 만들고 적절한 학습률을 설정해 기울기가 0인 지점을 구하는 것.
- 최적의 절편(b)을 구할 때도 동일하게 사용.
- a, b에 대해서는 각각 편미분
TensorFlow 가 제공하는 메소드를 이용
tf.train.exponential_decay()
tf.train.natural_exp_decay()
tf.train.polynomial_decay()
tf.train.inverse_time_decay()
tf.train.piecewise_constant()
- 다차원 편미분 개념 도입
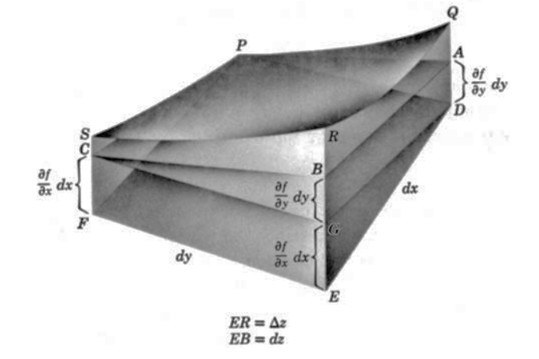
경사 하강법은 계산량이 커서 속도가 느리다.
확률적 경사 하강법은 데이터 일부를 랜덤하게 추출하여 일부 데이터만을 사용하기 때문에 속도가 빠르고 자주 업데이트할 수 있는 장점이 있다.
확률적 경사 하강법의 중간 결과는 진폭이 크고 불안정해 보일 수 있으나, 빠르게 최적해에 근사한 값을 찾아낼 수 있기에, 경사하강법을 대체해서 사용된다.
특히 모멘텀(momentum)을 이용하면, 지그재그 현상을 줄이면서 이동 방향에 관성을 더해 효과적으로 계산할 수 있다.










분쟁, 전쟁, 착취, 이기주의
