통계 이론 :: 표본 분포

1. 표본 분포

모분산이 알려진 경우 (비현실적, 이상적인 경우)

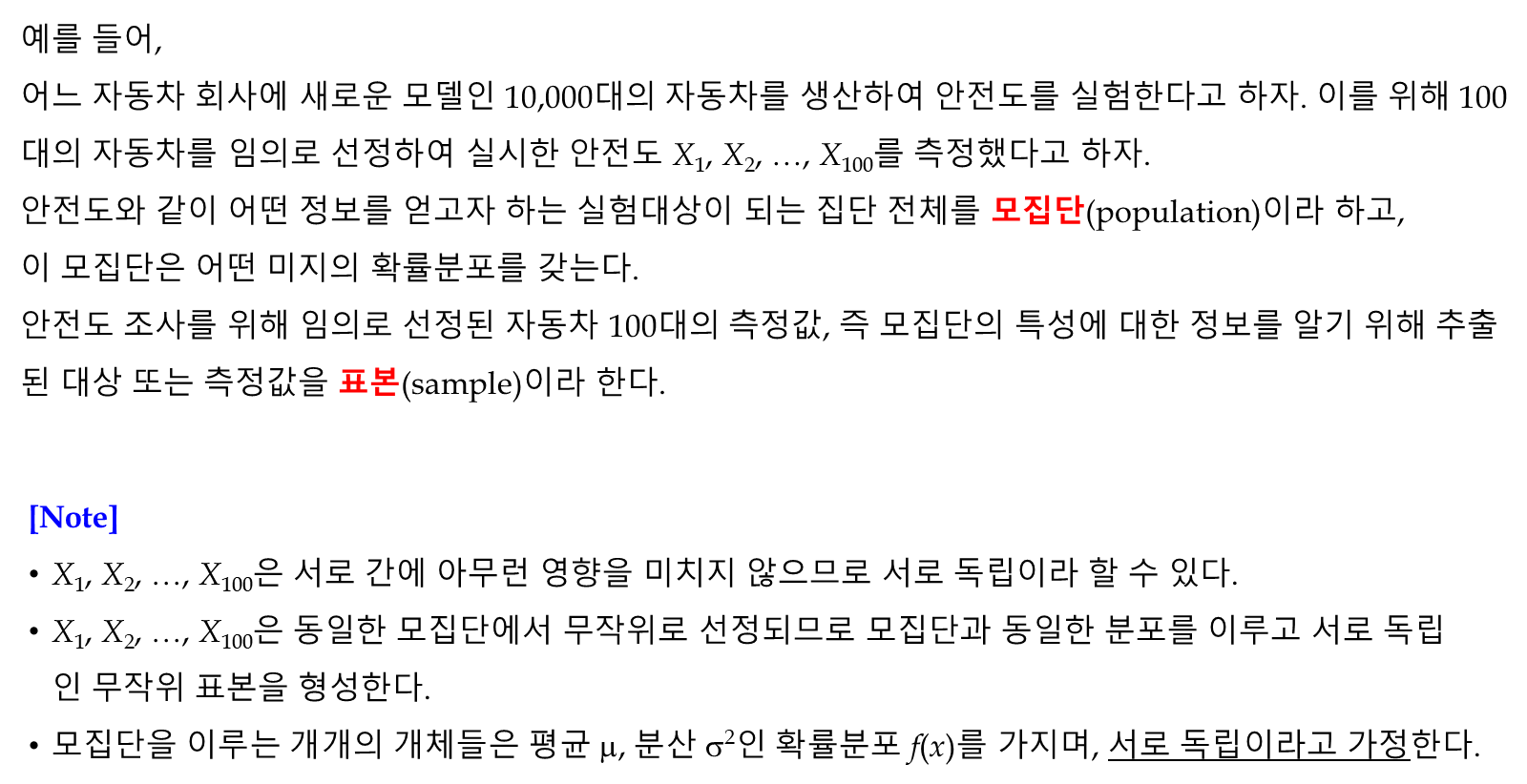
X1, X2 가 취할 수 있는 값은 각각 0, 1, 2, 3 이다. 표본평균 X의 확률분포를 구하기 위하여 X1, X2 의 결합분포를 생각하면, 위 표와 같이 나타낼 수 있다. 

한편,  X1, X2 가 취할 수 있는 값은 각각 0, 1, 2, 3 이므로, X의 관찰 가능한 값은 0, 0.5, 1, 1.5, 2, 2.5, 3 이므로, X1과 X2사이에는 아래와 같은 관계가 있다. 

 X=0    : (X1, X2 ) = (0, 0)

 X=0.5 : (X1, X2 ) = (0, 1), (1, 0)

 X=1.0 : (X1, X2 ) = (0, 2), (1, 1), (2, 0)

 X=1.5 : (X1, X2 ) = (0, 3), (1, 2), (2, 1), (3, 0)

 X=2.0 : (X1, X2 ) = (1, 3), (3, 1), (2, 2)

 X=2.5 : (X1, X2 ) = (2, 3), (3, 2) 

 X=3.0 : (X1, X2 ) = (3, 3)

따라서, X의 확률분포는 아래 표와 같다.

 

 

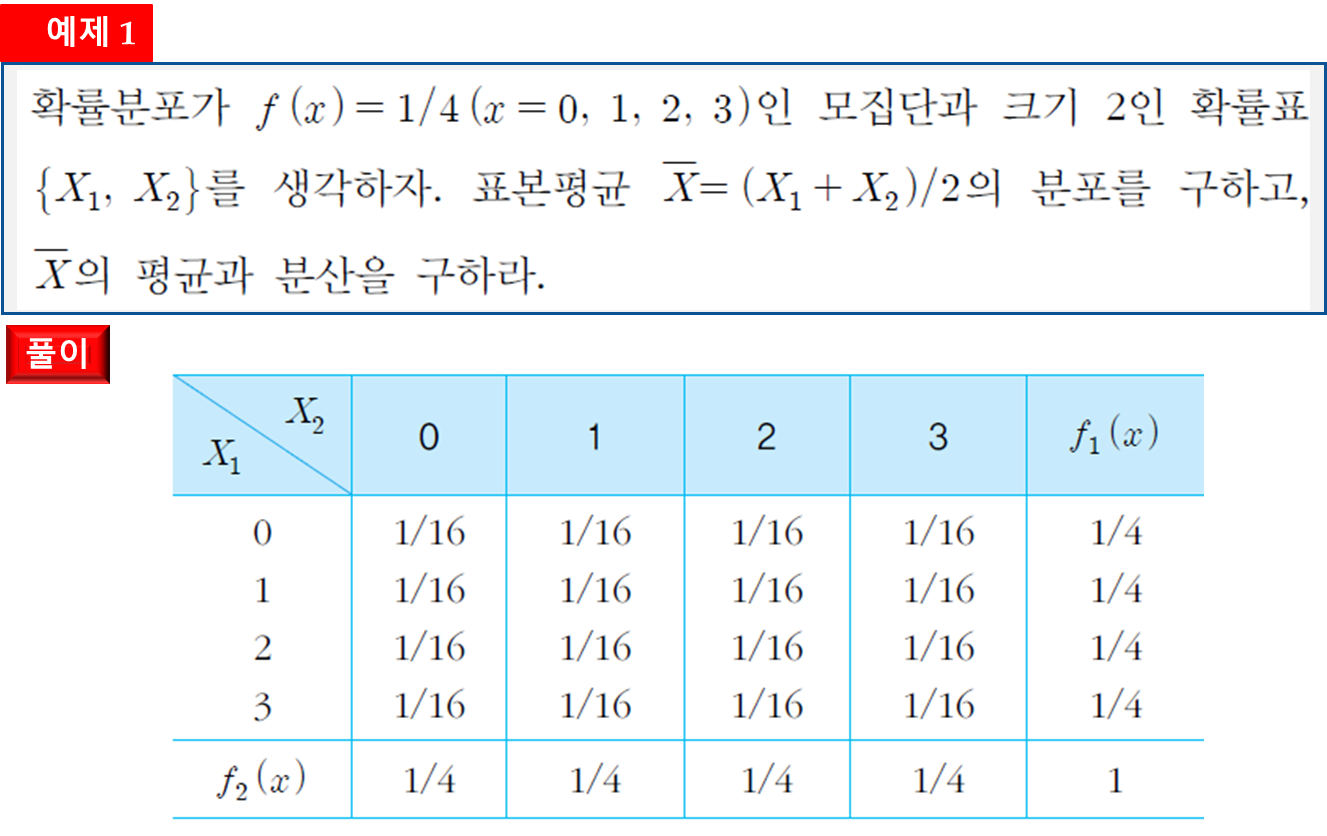
중심극한 정리와 표본평균의 표본분포 비교

(참고) 표본 비율을 특정할 수 없는 경우, 1/2 로 지정한다. 

 

 

 

2. 카이제곱분포

모평균을 추정하기 위해 표본평균을 사용

모분산을 추정하기 위해 표본분산을 사용

모평균 추론을 위해서 표본평균의 분포를 알아야

모분산 추론을 위해서 표본분산의 분포를 알아야

 

카이제곱분포

감마분포에서 α=n/2, β=2 인 특수한 경우를 자유도 n인 카이분포라고 한다.

모순산이 특정한 값을 갖는지 여부를 검정하는데 사용하는 분포

두 범주형 변수간의 연관성을 검정하는데 주로 사용

 

 

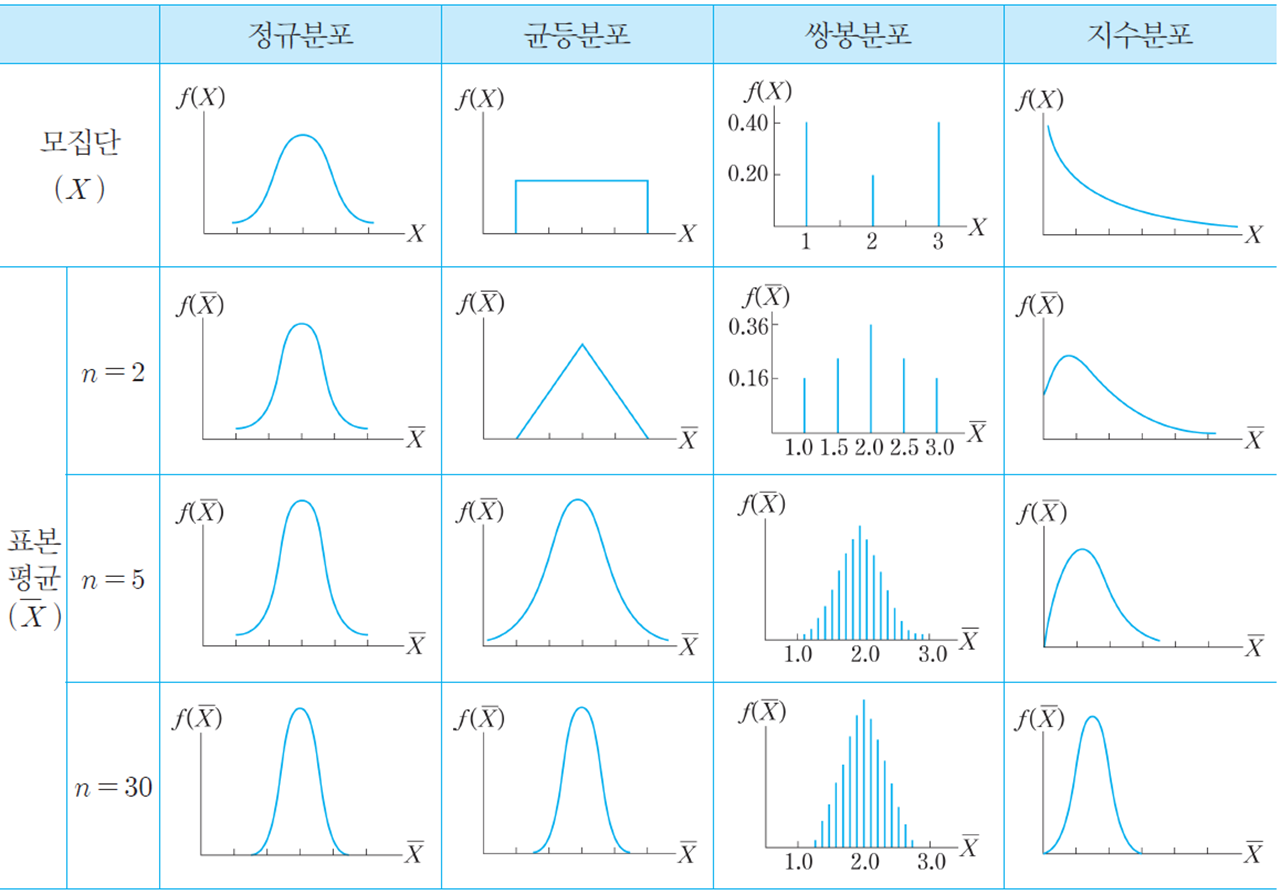
카이제곱분포 만들기

1. 표준정규분포에서

2. 변수 한 개(자유도 1) 를 랜덤하게 추출

3. 그 변수를 제곱해서 히스토그램으로 표현

이 과정을 반복하면, 아래 양의 히스토그램.

 

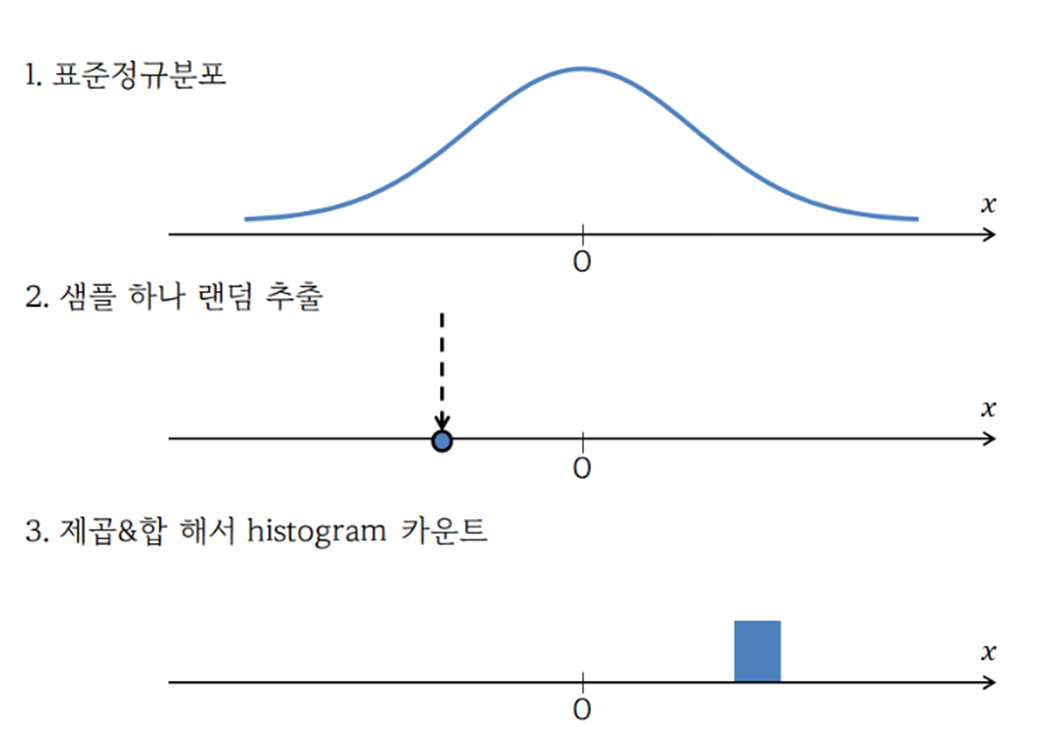
한번에 추출하는 변수가 2개 이상, 즉 자유도 2개 이상이면, 변수들을 각각 제곱해서 더함. 따라서, 더해주는 변수가 많아질 수록 정규분포에 접근(중심극한 정리)

카이제곱 분포 응용

일반적으로 오차(error)는 정규분포로 만들어 두기 때문에 오차 또는 편차를 분석할 때 유용.

샘플수가 무수히 많고 합을 이용해 오차를 정의하는 경우, 오차의 분포를 정규분포를 따름(중심극한 정리)

오차나 편차가 우연히 발생할 수 있다고 볼 수 있을 만한 수준인지 아닌지 판별할 수 있다.

그림 예. 회귀분석 시, 샘플링 데이터는 정규분포에서 랜덤하게 샘플링 되어 얻은 값이라고 가정

 

 

 

 

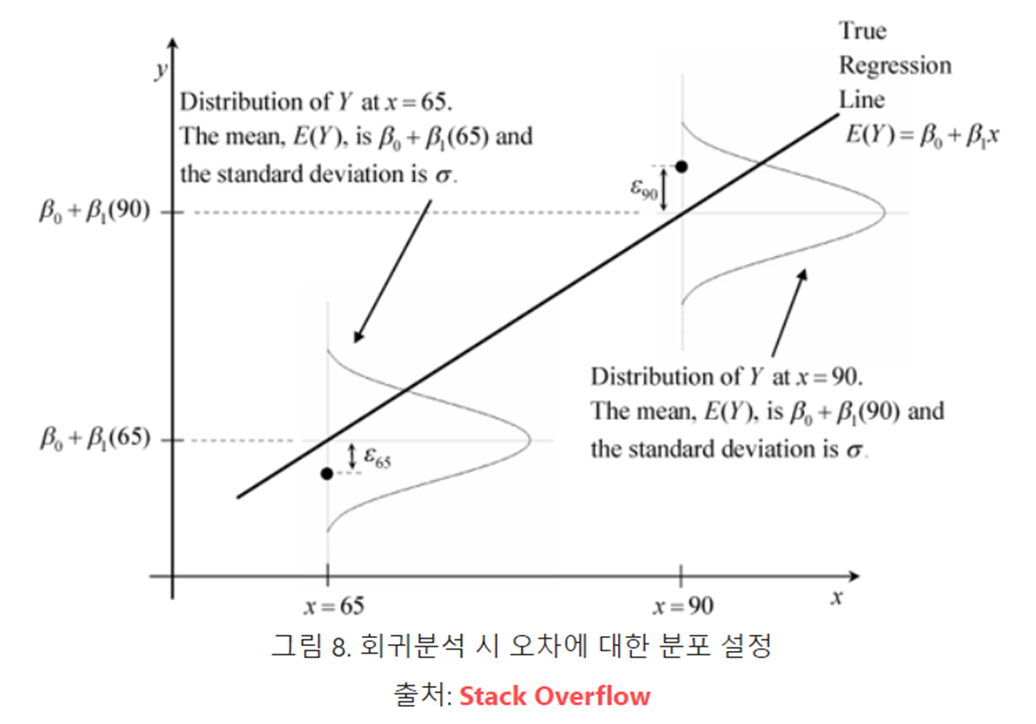
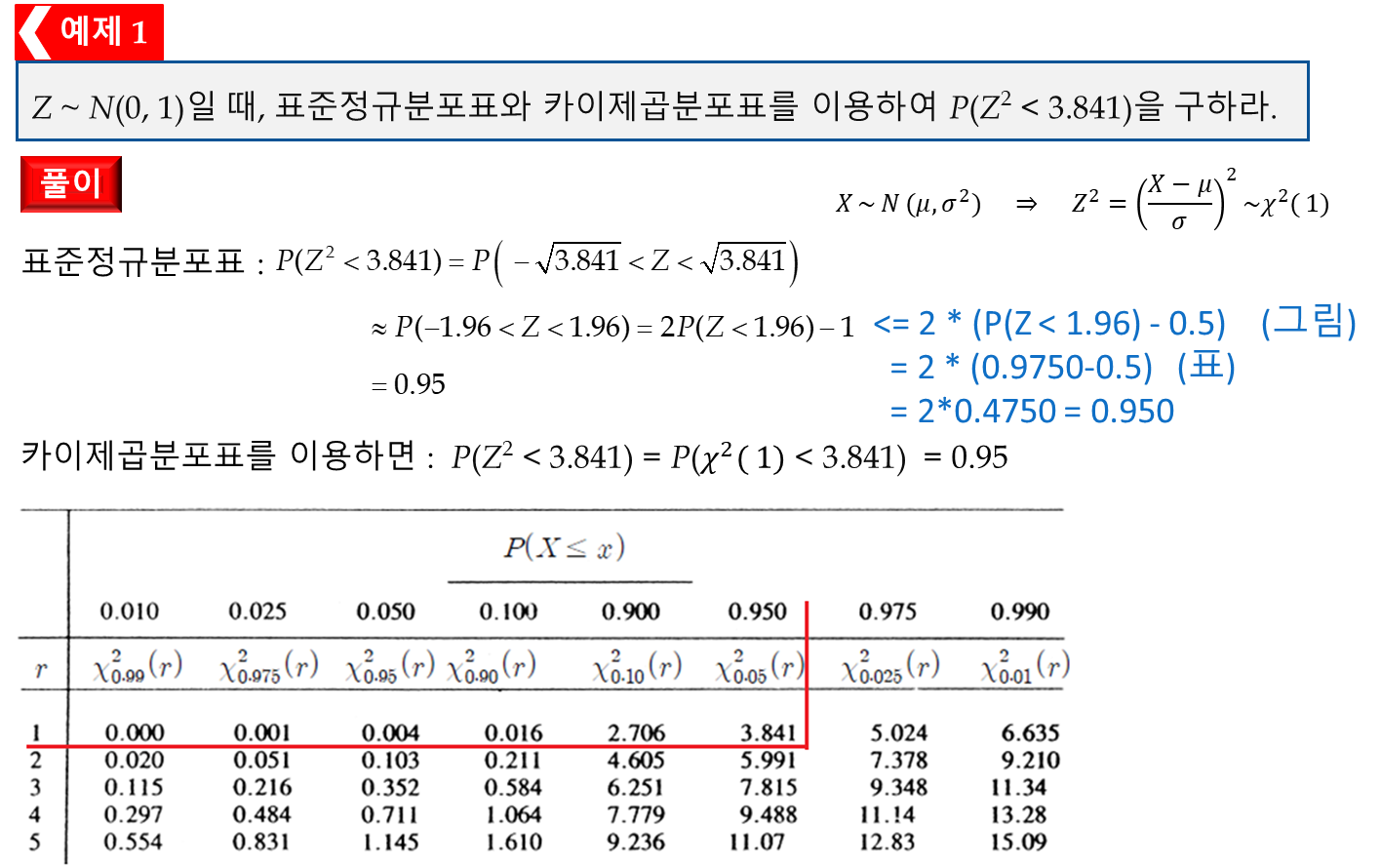
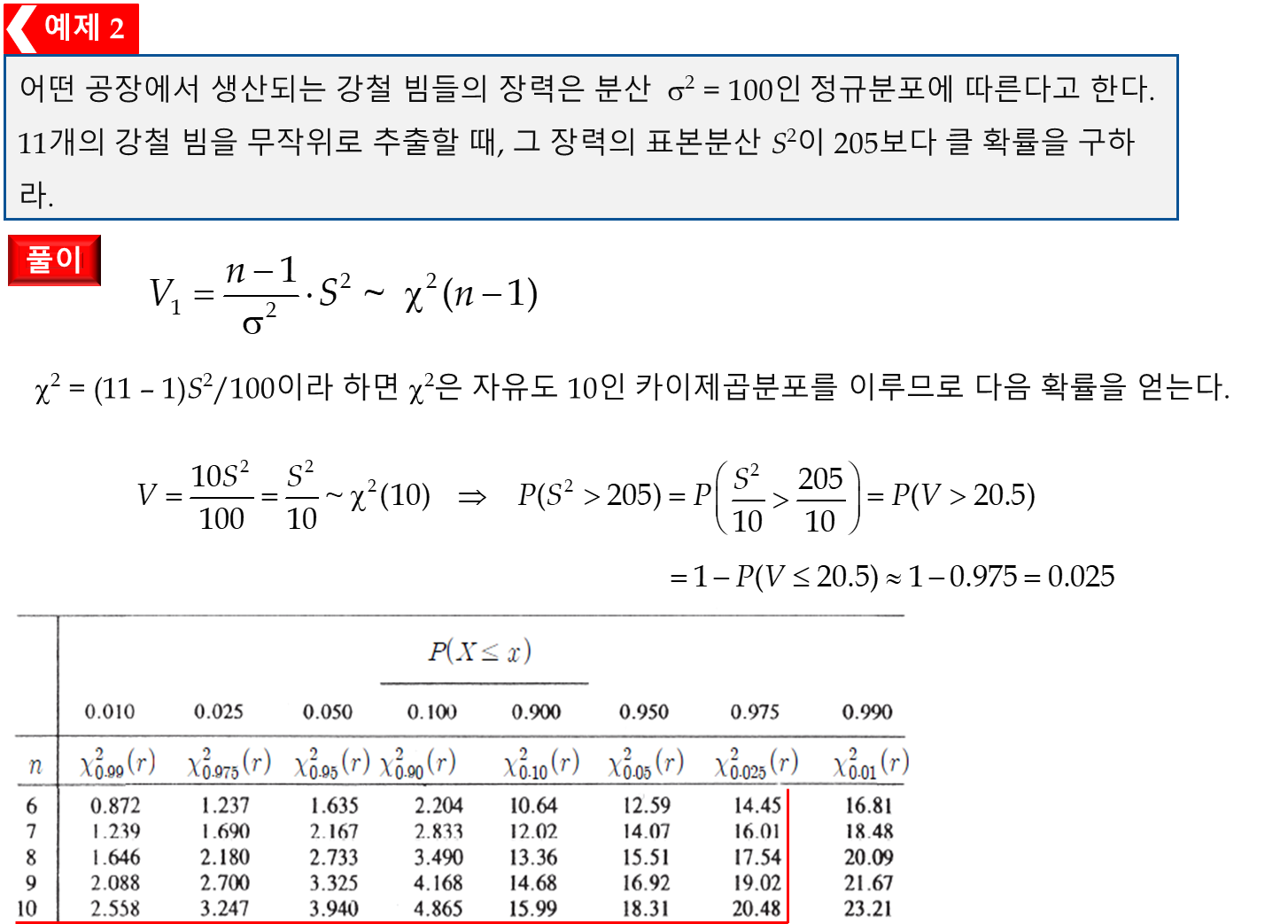
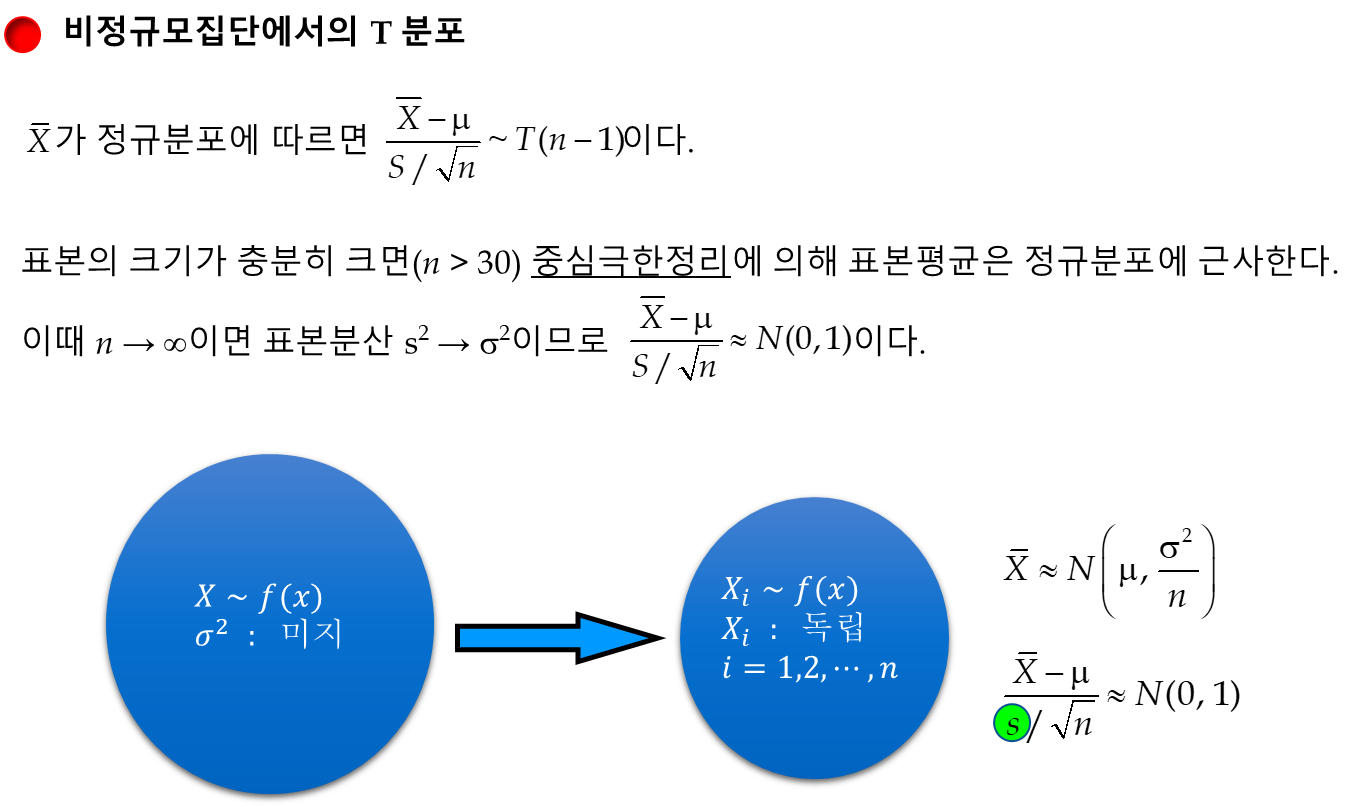
3. T 분포 

모분산이 알려지지 않은 경우 (현실적인 경우)

 

 

 

 

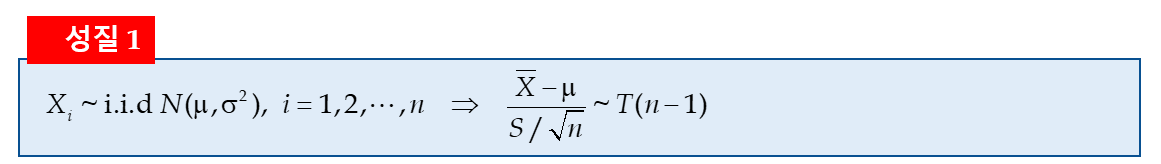
정리