728x90
반응형
나비아-스토크 방정식 (Navier-Stokces equations) - 평균류
뉴턴의 운동 제2법칙, 운동량 보존 법칙으로부터 유도된, 자전하는 지구 상에서의 유체의 힘의 균형을 나타내는 N-S 방정식은 아래와 같다
아래 식 유도는 Holton 역학책 Boussinesq Approximation 에서 유도한 식.
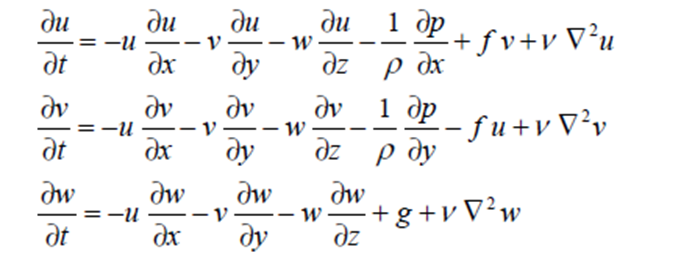
좌(1)항: 유체 요소에 가해지는 국지 가속으로 발생하는 관성력 (국지항)
우(1-3)항: 유체 요소에 가해지는 이류 가속으로 발생하는 관성력 (이류항)
우(4)항: 유체 요소에 작용하는 기압경도력 (PGF)
우(5)항: 유체 요소에 작용하는 겉보기 힘 (코리올리 힘 또는 가속도),
우(6)항: 유체 요소에 작용하는 점성력 또는 마찰력 (점성항)
좌(1)항과 우(1-3)항을 합치면 전미분 형태로서 tendency term으로 불림
난류항은 난류 및 레이놀즈 응력항이 적용되어야 함.
N-S 방정식은 이차 계수의 비선형 편미분 방정식이고, 비선형인 관성항과 점성항으로 인해서 이 방정식의 해석해를 구하는 것은 불가능. 따라서 차분을 이용한 수치해석 방법으로 근사치를 구한다.
각 항들은 경우에 따라 아래와 같이 생략하여 해석할 수 있다.
1. 정상류 (steady flow) 인 경우, tendency term --> 0.
2. 수평적으로 균질한 지표면 상에서, 이류항 --> 0.
3. 고/저기압 가운데나 미규모 운동인 경우, PGF --> 0.
4. 적도에서, Co.F term --> 0.
5. 점성항을 무시하면, 비점성 (또는 이상적인) 유체에 대한 오일러 방정식이 됨.
728x90
반응형