거칠기 길이 (Roughness length)
식 (4) 를 다시 쓰면,

(7)
식 (3)과 합치면,

(8)
식 (1)의 상수 A는 아래와 같이 정의된다.

(9)
따라서, 식(2)는 아래와 같이 쓸수 있다.

(10)
z = 0 이면, ln 0 = -∞이기 애문에 u = - 무한 이 되므로 비현실적인 조건. 따라서, 식 (10)은 거칠기 길이 (z0)라 불리는 최소 고도에서만 의미가 있다.
적분상수 B를 결
정하기 위해서, 식(10)에서 u(z0)=0, 즉 z0에서 풍속은 0이라는 조건을 붙인다.

(11)
따라서, B는 아래와 같이 정의된다.

(12)
식 (12)를 식 (10)에 대입하면,

(13)
결과적으로 아래 식이 된다

(14)
따라서, 마찰속도와 거칠기 길이 식에 의해 경계층의 어떤 고도에서도 바람을 구할 수 있다. ln z에 대하여 u는 ln z 축의 절편은 z0이고, 기울기는 k/u* 인 선형관계가 된다.
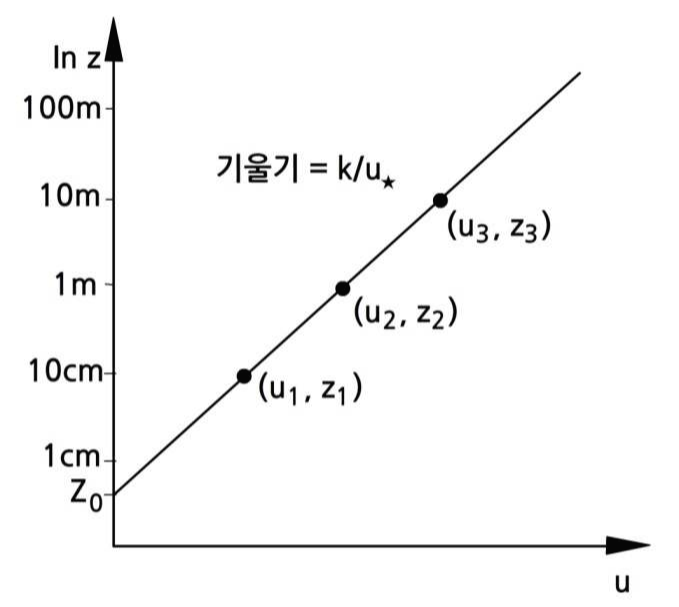
그림 4. 경계층에서 u와 ln z 의 선형관계
마찰속도와 거칠기 길이는 서로 다른 고도에서 관측된 두 개 이상의 바람 관측치로부터 구할 수 있다. (그림 4). 그리고 마찰속도를 가지고, 식(6)에 의하여 운동량 플럭스 또는 전단응력을 계산할 수 있다.
거칠기 길이는 윈드프로파일(Wind Profile)에서 풍속이 0인 고도(높이)로 정의될 수 있다. 거칠기는 공기역학 텍스트에서 자주 사용되는데, 지표의 높이, 형태, 저항 등, 즉, 지면 등의 거칠은 정도를 말한다. 지표의 종류에 따른 거칠기 길이는 아래 표 1과 같다
표 1. 지표의 종류에 따른 거칠기 길이

아래 그림은 3종류의 다른 지표의 경우 윈드 프로파일.
아래 식에 의해서, 어떤 고도에서라도 거칠기 길이가 클 경우 바람 u(z)는 더 작다(식 (11.14)).

또한, 미끈한 지표에서의 경계층 높이는 거친 지표일 경우만큼 높게 발달하지 않는다.
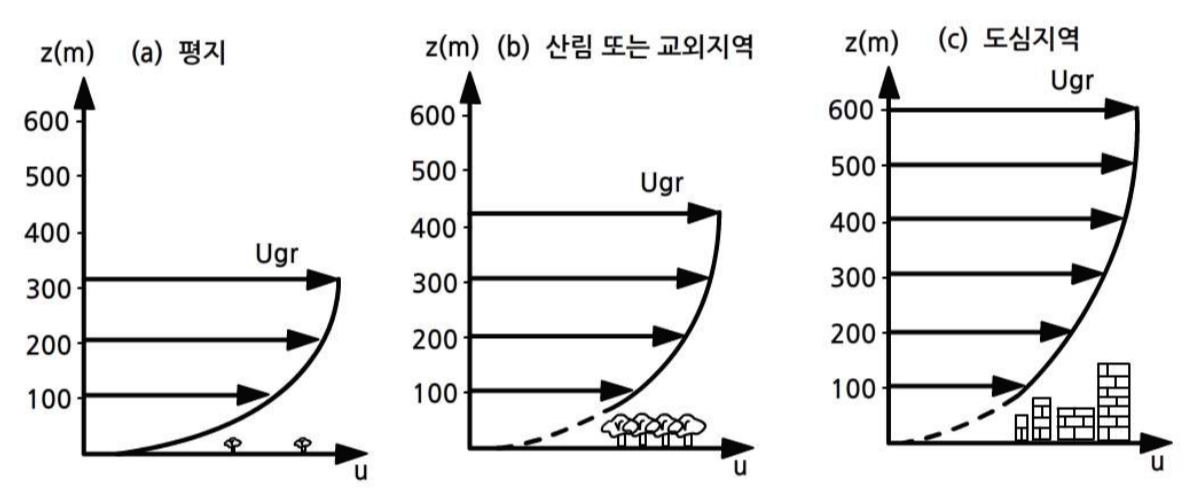
그림 5. 지표 거칠기에 따른 풍속의 연직 변동: (a) 매끈한 지표, (b) 적당히 거친 지표, (c) 매우 거친 지표
영면변위 (Zero plane displacement)
식생 높이의 활성 표면은 에너지 변동이 발생하는 중요한 곳으로 정의된다.
식생 꼭대기 부근에서는 기류를 방해하는 항력(drag)이 발생할 것이다. 식생 위에서의 바람은 대수법칙에 따르며, 식생 꼭대기 부근에 위치한 식생상부층 ‘영면변위(d)’에서는 마치 지표면에서와 같은 흐름의 양상을 보여준다(그림 6). 즉, d는 식생 꼭대기 부근에서 식생에 의해 발생하는 항력을 나타낼 수 있다. 실례로, 식생이 매우 밀집되어 있는 경우, d=2h/3이다. 그러므로 d는 대부분의 식생에서 매우 유용한 풍속의 함수이다.

그림 6. 식생높이(h)에서의 전형적인 윈드프로파일과 고도(d)에서의 영면변위 개념.
이러한 식생에서의 윈드프로파일의 영향을 고려하여 식 (11.14)는 다음과
같이 나타낼 수 있다. 이론적으로 (d+z0)에서 풍속은 0이나, 실제로 에서의 풍속은 0까지 떨어지지 않는다.
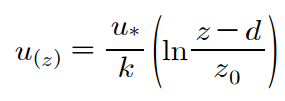
다른 거칠기를 갖는 지표에서의 기류
거칠기 길이 z01의 지표에서 z02의 지표까지의 기류 때문에 발생하는 운동량의 변화는 윈드프로파일의 점차적인 상향 변화를 야기한다 (그림 7). 내부 경계층은 수 km에 달하는 수평 취송거리(페치, Fetch)의 함수로서 다른 거칠기의 지표에 의해 변한다.
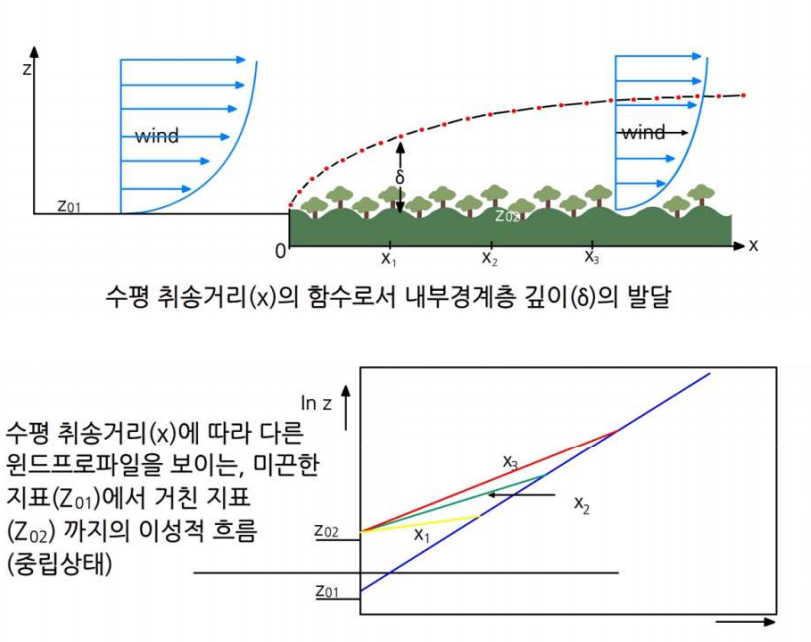
그림 7. 취송거리의 함수로서 내부 경계층의 성장
그러므로, 다양한 거칠기를 갖는 지표가 연속적으로 존재할 때, 내부 경계층은 아래 그림 8과 같이 매우 복잡하게 발달한다.
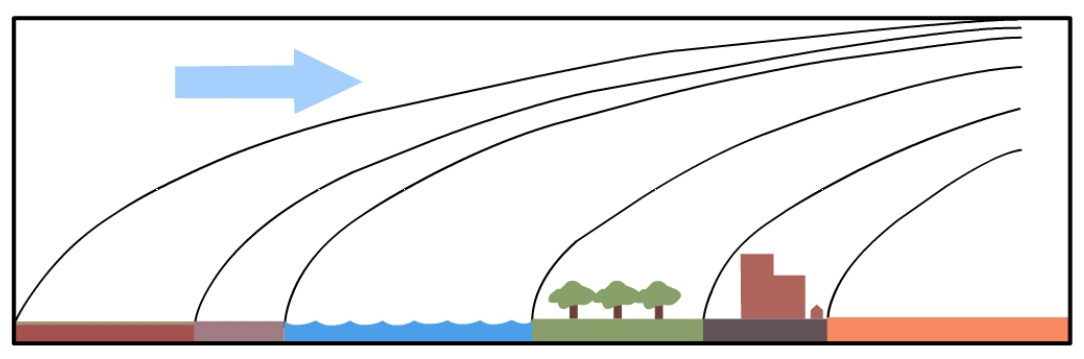
그림 8. 복합 형태의 지표일 경우, 내부 경계층의 전형적인 흐름
자료 출처: 기상청