주어진 표현식의 결과를 구하여라
1) 2+3/5
2) (2+3)**2
3) 25.01**1/2
4) (2.0 + 3**2 ) /( 8-2+1)
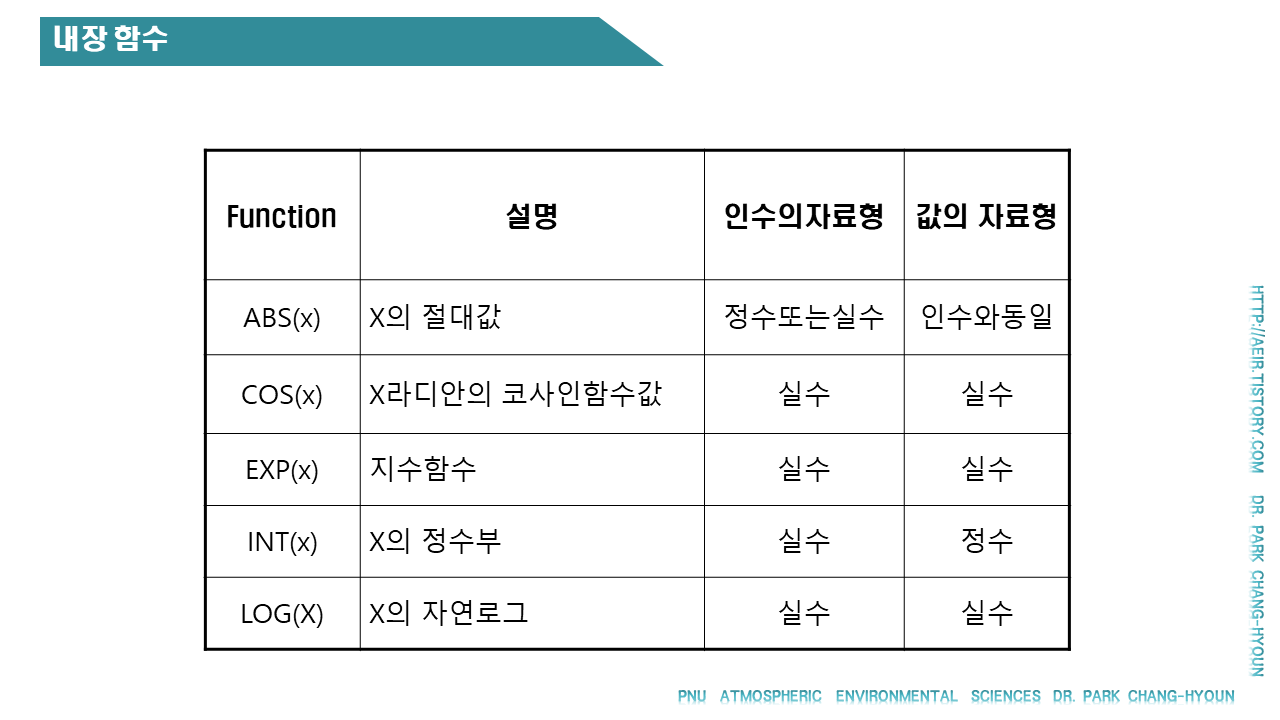
5) abs (1-2-4)
6) int (5.0 + 4.0/ 3.0 )
7) "one"//"two"
아래 주어진 변수에 대한 다음 표현식의 결과?
TWO=2.0 & THREE=3.0 & FOUR=4.0 &
IntEight=8 & IntFive=5 & Str_1 = “For” &
Str_2 = “tran” & Label_1=“foot”
Label_2=“lbs”
1) TWO+THREE * THREE
2) IntFive/3
3) (THREE+TWO/ FOUR )**2
4) IntFive**2 / TWO**2
5) Str_1//Str_2//"-90"
6) Label_1//" "//Label_2
7) Str_2(2:3)//"ndom"
다음 식을 fortran 표현식으로 써라
1) 10+5B-4AC
2) A2 + B2 – 2AB cos T
다음 식의 계산값을 구하는 fortran 프로그램을 작성하시오.
1) Y=7x4 + 3x3 + 4x2 + 2x + 1
2 )x=40, y=?
과제
아래 문제를 해결하는 코드를 작성해 봅시다. (내장함수 이용)
1. 정수 17을 실수로 변환 (아래 예제 코드 참고)
i = 17
gi = i
write(*,*) gi
2. 실수 23.67을 정수로 변환
3. 125의 1/3승값
4. -136.35의 절대값
5. √289 값 구하기
6. 정수 6971 실수화
7. 3161.89 정수화
8. 19.825 소수부 절단
9. -31.695 소수부 절단
10. 37을 5로 나눈 나머지 구하기
11. 정수 113, 216, 351, 679, 823 중 최대값
12. 실수 32.95, 86.45, 21.33, 69.28, 19.81 중 최대값
13. 실수 19.3, 21.2, 13.6, 37.6, 37.8, 27.9 중 최소값
14. 정수 198, 321, 439, 691, 113 중 최소값
15. 83과 -21 중 -21의 부호를 83에 넘겨주기
16. e5
17. ln 1.7 (= loge 1.7)
18. log 8.5 (= log10 8.5)
19. sin 75° (주의 radian 이 아님)
20. cos 35°
21. tan 25°