728x90
반응형
상사이론
중립대기는 일반적으로 발생하기 힘든 조건이다. 중립 대기에서, 지표층은 지수 바람 분포에 의해서 특성화되고, 높이에 따라 운동량 플럭스와 난류 속도 변동의 표준편차가 균일하게 분포된다.
대기-지표면 사이의 열의 난류교환은 지표층을 열성층(thermal stratification)으로 만들고, PBL전체를 열성층로 만든다.
성층화된 지표층의 평균 및 난류 구조를 정량적으로 기술하기 위한 이론적 또는 반경험적인 개념을 찾는 것이 중요하므로, 상사이론을 도입한다.
상사이론들
- Monin-Obukhov similarity
- Mixed-layer similarity
- Local similarity
- Local free convection similarity
- Rossby-number similarity
모닝-오브코프(Monin-Obukhov) 상사 이론은 현재까지 가장 만족스러운 접지층에서의 상사개념이다. 또한 직접 측정자료가 없는 곳에서의 미기상학 정보를 예측하는데도 유용하다.
Monin과 Obukhov 가 제안한 상사 가설
M-O 상사관계에서는, 접지층에서의 평균 흐름과 난류 특성은 다음의 4개 독립변수에만 의존한다고 가정한다.


M-O 상사관계의 가정
(1) 수평적으로 균질, 정상상태(stationary)인 기층 (즉, z만의 함수로 표현됨)
(2) 운동량과 열 난류 플럭스는 높이(z)에 따라 일정
(3) 분자교환은 난류교환과 비교해서 무시 가능
(4) 회전효과는 지표층에서 무시.
(5) 지표면 거칠기, 경계층 높이, 지균풍의 영향은 아래 식으로 모두 설명됨.

앞의 4가지 독립변수는 3가지 기본 차원 (길이, 시간, 온도)를 포함하므로, 버킹엄 파이 정리를 이용하면, 아래와 같이 단 하나의 독립 무차원 그룹으로 공식화 할 수 있다. (전개 생략)
오브코프 길이는 난류 흐름에 대한 부력의 영향을 설명하기 위한 것인데, 특히 대기 경계층의 10분의 1 이하 지표경계층에서 사용된다. 1946년 알렉산더 오부호프에 의해 처음 정의되었다. 모닌과 오브코프가 개발한 상사이론에서 중요한 역할을 하기 때문에 모닌-오브코프 길이로도 알려져 있다.
오브코프 길이 (L) 정의
- 난류가 바람시어보다 부력에 의해 더 많이 발생하는 높이
- 시어(마찰효과)가 중요한 지표면 부근 역학(기계적)난류층의 두께
- 역학난류 층의 두께 또는 역학난류 아층의 특성높이(규모)
- L의 범위 ( -∞ < L < ∞ )

L에 대한 물리적 해석
모닌-오브코프 상사 이론를 바탕으로 해석된다.
낮 동안 -L은 난류 운동 에너지(TKE)의 부력 생산이 바람의 전단 작용(TKE의 전단 생산)에 의해 생성되는 것과 동일한 높이이다.
오브코프 길이는 일반적으로 1에서 수십 미터 정도
- 안정 대기: 양
- 불안정 대기: 음
- 중립대기 : 무한
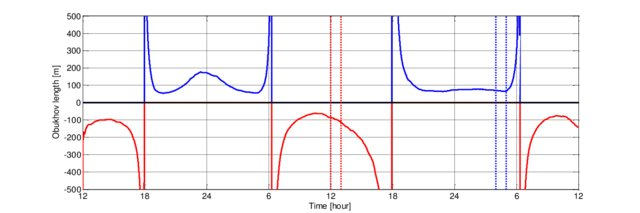
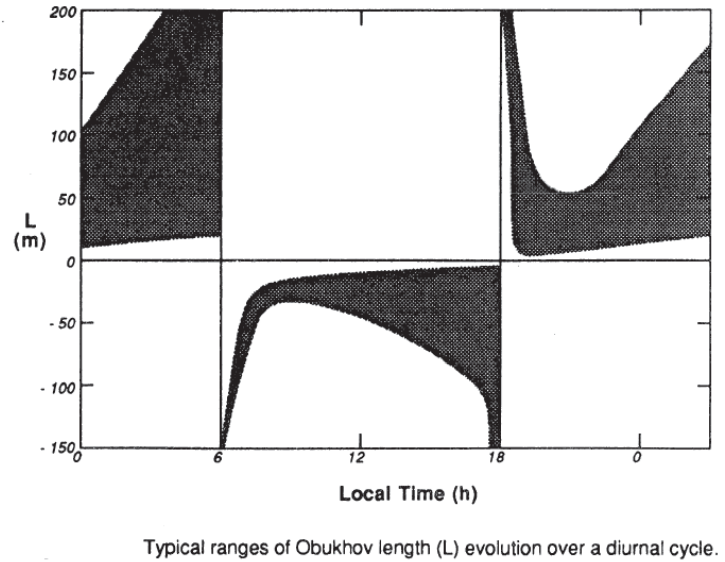
아래 그림은 육지의 맑은 날씨 조건에서 오브코프 길이의 전형적인 일변화를 나타낸다.
리차드슨 수와 비교
아래 식은 부력효과와 시어효과의 중요성을 측정하는 매개변수로서 리차드슨 수와 유사하다. 지표면으로 부터 고도가 높아지면서 부력의 중요성이 증가한다. 따라서, z/L는 높이에 따라 선형으로 변한다.
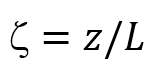
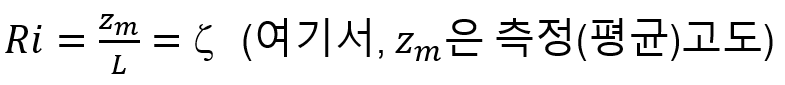

연습문제
기상직 5급 공채 - 미기상학 (2017)
aeir.tistory.com
728x90
반응형